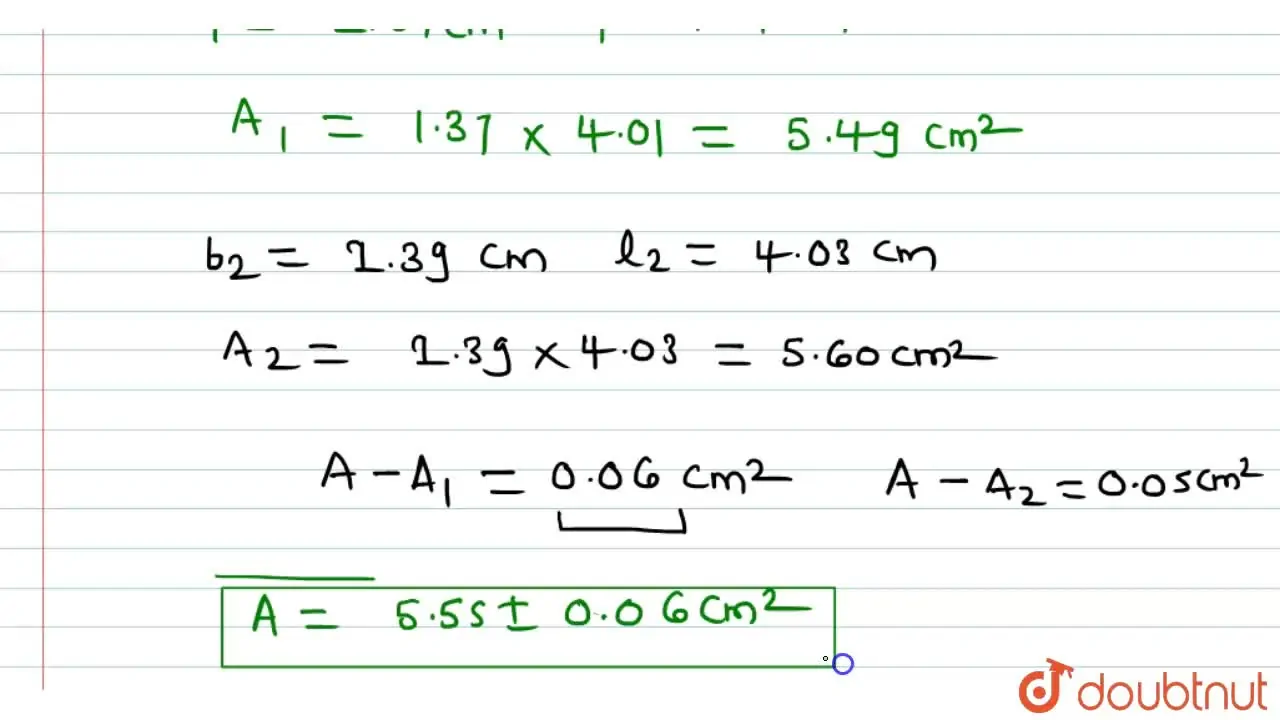A vernier callipers is used to measure the width and the length of a rectangular plate. The measured values are 1.38 cm and 4.02 cm respectively.Find the uncertainly in the value of its area.
Given that, width w=1.38 cm
length , l=4.02 cm
Since the least count of a vernier callipers is 0.01 cm, each of the above mentioned measurements has an uncertainly of ±0.01 cm. hence, the values can be written as
w=1.38 cm ±0.01 cm
l=4.02cm±0.01cm
The area obtained using the measured value is A=w x l
= 1.38 x 4.02
A=5.55cm2 ....(i)
If we take the lower limits of both the measured values i.e.
lmin=4.02-0.01
=4.01 cm
and wmin=1.38-0.01
=1.37 cm
The minimum possible area (lower limits of the area ) comes out to be Amin=4.01×1.37cm2
Amin=5.49cm2...(ii)
The upper limit can also be calculated similarly.
∴Amax=4.03×1.39cm2
Amax=5.60cm2 ...(iii)
using equation (i),(ii) and (iii) , we find that Amin is lower than A (the nominal measurement ) by the value 0.06cm2
And Amax is higher than A by the value 0.05cm2
As a practical rule, we choose the higher of these two deviations (from the measured value ) as the uncertainly, in our result.
Therefore, in this particular example, we can write the area of plate as 5.55cm2±0.06cm2
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Try Yourself82videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION A Objective (One option is correct )50videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)10videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))1videos
WAVE OPTICS
Similar Questions
The length and breadth of a rectangular plate are measured to be 14.5 cm and 4.2cm respectively. Find its area to appropriate significant figures.
View SolutionLength and breadth of a rectangular table-top are 36 cm and 24 cm respectively. Find its perimeter
View SolutionThe refractive index of the material of the prism and liquid are 1.56 and 1.32 respectively. What will be the value of θ for the following refraction ?
 View Solution
View SolutionThe length and width of a rectangular plate are (16.30±0.05) and (13.80±0.05) cm respectively. Calculate the area of the plate and also find the uncertainty in the area.
View SolutionThe internal and external diameters of a hollow cylinder are measured with the help of a Vernier callipers . Their values are 4.23±0.01cmand3.87±0.01cm, respectively . The thickness of the wall of the cylinder is
View SolutionThe internal and external diameters of a hollow cylinder are measured with the help of a Vernier callipers . Their values are 4.23±0.01cmand3.87±0.01cm, respectively . The thickness of the wall of the cylinder is
View SolutionThe length and breadth of a plate are (6±0.1)cmand(4±0.2)cm respectively. The area of the plate is
View SolutionTwo identical satellites are moving around the Earth in circular orbits at heights 3R and R respectively where R is the radius of the Earth. The ratio of their kinetic energies is x. Find x.
View SolutionThe length and breadth of a rectangular are 25 cm and 10 cm respectively and were measured to an accuracy of 0.1 cm. The percentage error in area is
View SolutionThe length and breadth of a rectangle are (5.7±0.1)cmand(3.4±0.2)cm, respectively calculate the area of rectangle with error limits.
View Solution