A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then 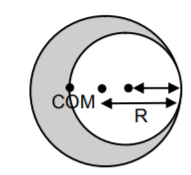
(R2+R+1)(2–R)=1
(R2–R–1)(2–R)=1
(R2–R+1)(2–R)=1
(R2+R–1)(2–R)=1
The correct Answer is:A
NA
Related Playlists
Similar Questions
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
 View Solution
View SolutionA uniform charged hemisphere of radius b and charge density ρ has a hemispherical cavity of radius a(a=b2) cut from its centre . If the potential at the centre of the cavity is nρb216∈0 then n = ?
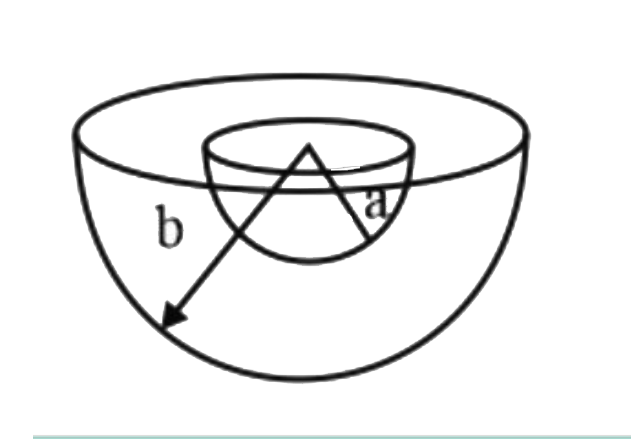 View Solution
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
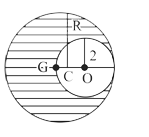 View Solution
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 View Solution
View SolutionA uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
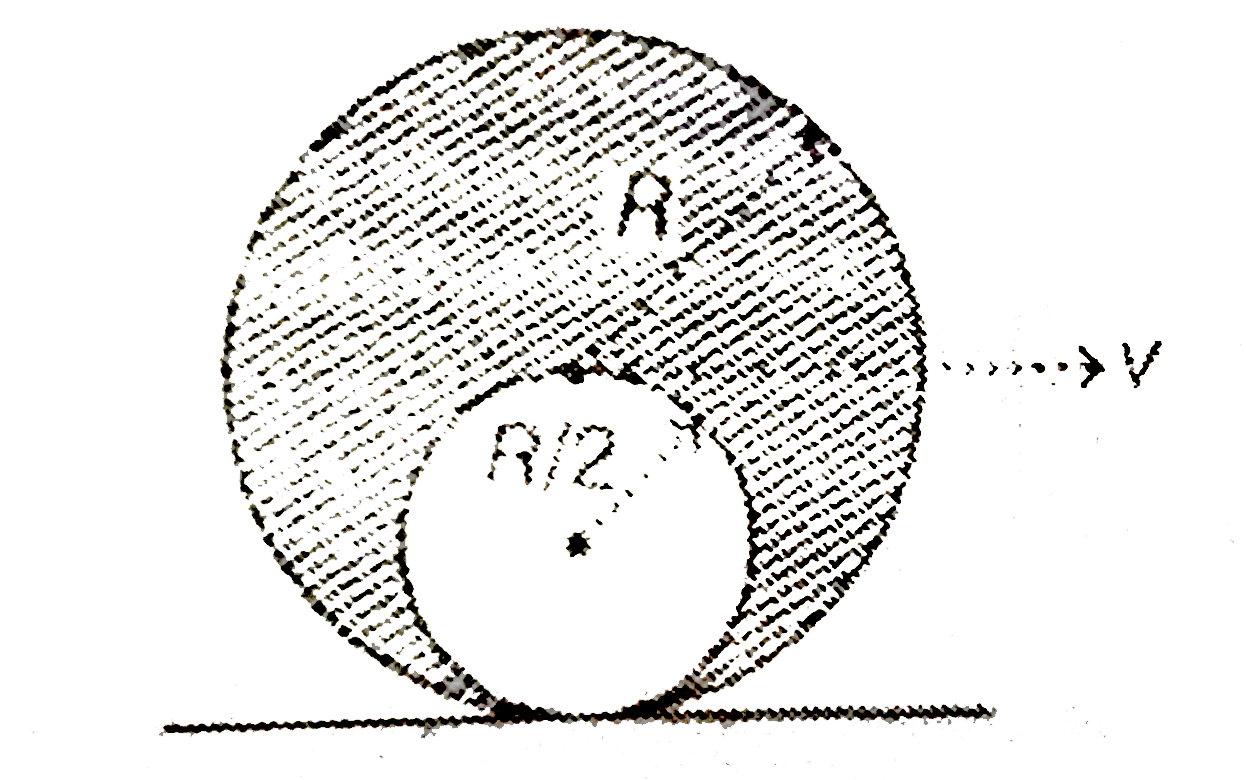 View Solution
View SolutionA uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View Solution


