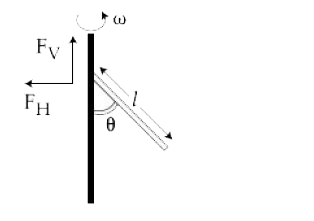
A uniform rod of length 'l' is pivoted at one of itd ends on a vertical shaft of negligible radius When the shaft rotates at angular speed ω the rod makes an angle θ with it (see figure) . To find θ equate the rate of change of angular momentum (direction going into the paper) ml212ω2sinθcosθ about the centre of mass (CM) to the torque provided by the horizontal and vertical forces FH and FV about the CM. The value of θ is then such that :
Option1 cosθ=g2lω2
Option2 cosθ=3g2lω2
Option3 cosθ=glω2
Option4 cosθ=2g3lω2
Step by step video & image solution for A uniform rod of length 'l' is pivoted at one of itd ends on a vertical shaft of negligible radius When the shaft rotates at angular speed omega the rod makes an angle theta with it (see figure) . To find theta equate the rate of change of angular momentum (direction going into the paper) (ml^2)/(12) omega^2 sin theta cos theta about the centre of mass (CM) to the torque provided by the horizontal and vertical forces F_H and F_V about the CM. The value of theta is then such that : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions

A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
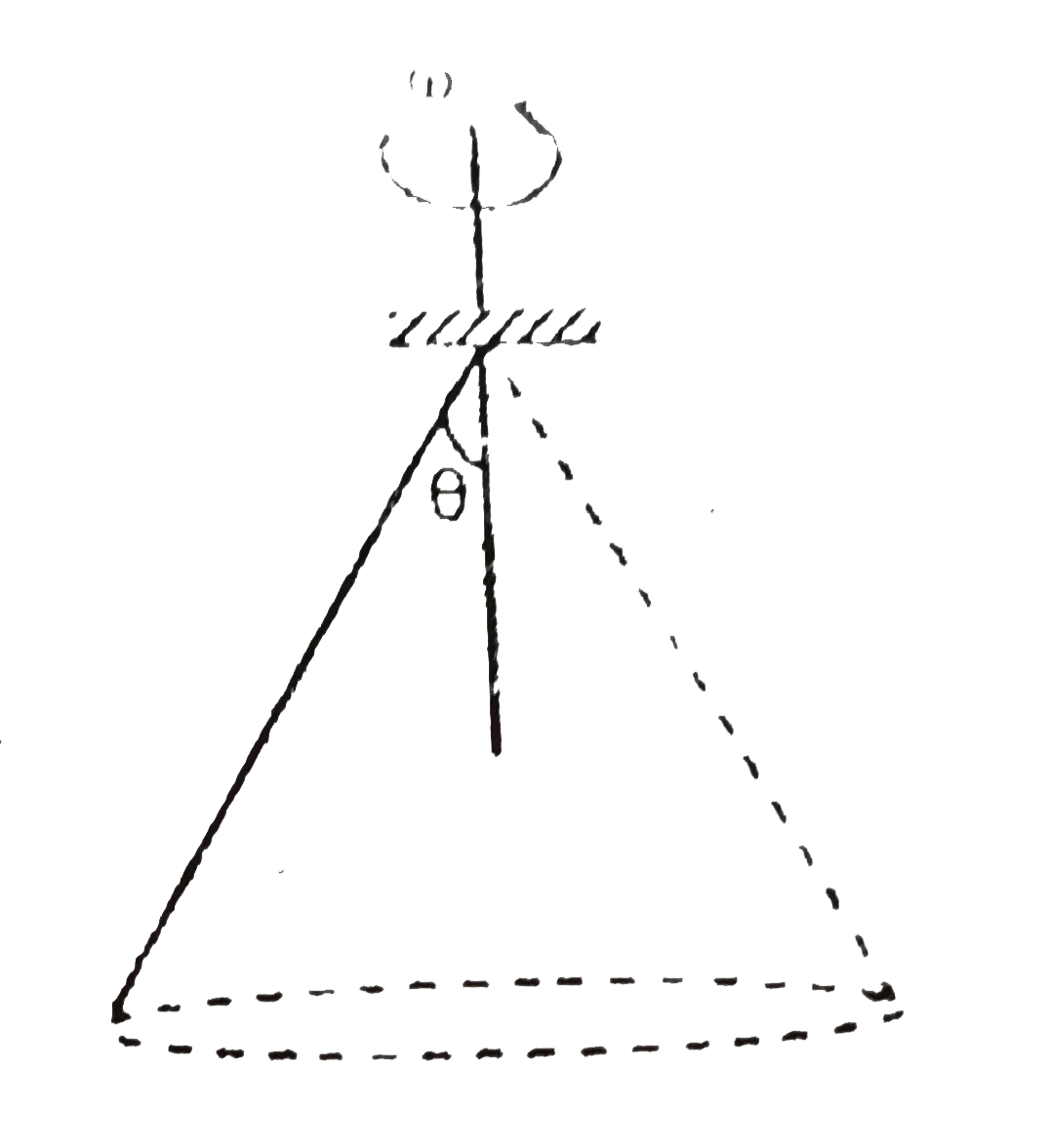
b. What is the tangential linear acceleration of the free end when the rod is horizontal?View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 View Solution
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
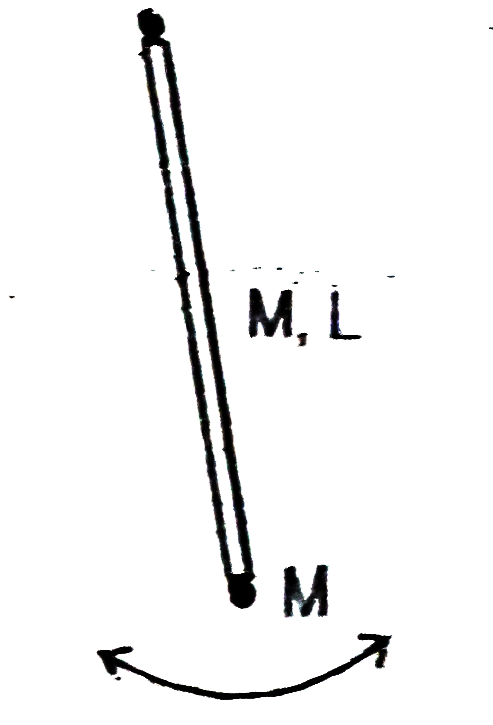 View Solution
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 View Solution
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?
 View Solution
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .View Solution
.View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.
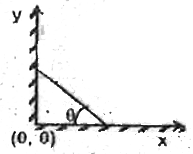 View Solution
View Solution


