A uniform equilateral triangular lamina of side a has mass m. Its moment of inertia about the axis passing through the centroid and prependicular to the plane of the lamina is :-
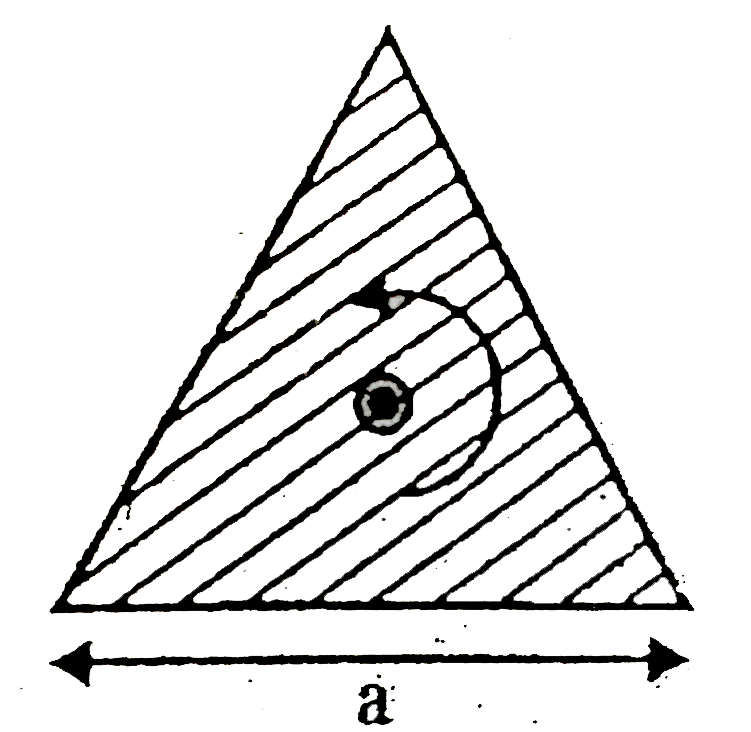
The correct Answer is:A
Any uniform triangular lamina can be represented by three point masses for purpose of calculation of moment of inertia.
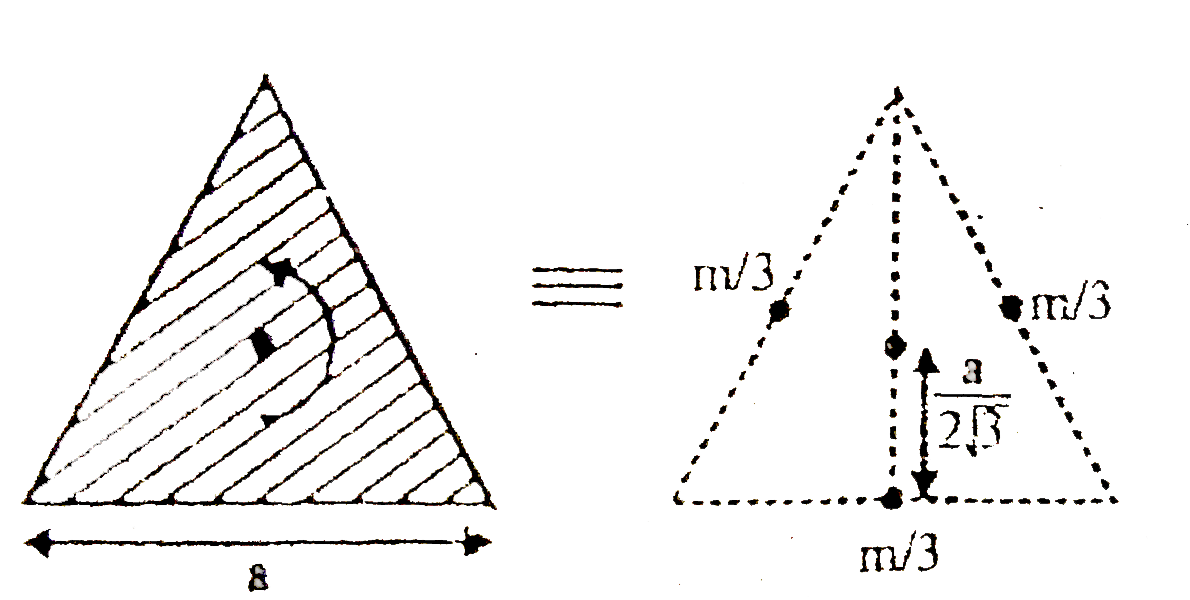
Required moment of inertia
Related Playlists
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 260videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 399videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS44videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionA uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionFor the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
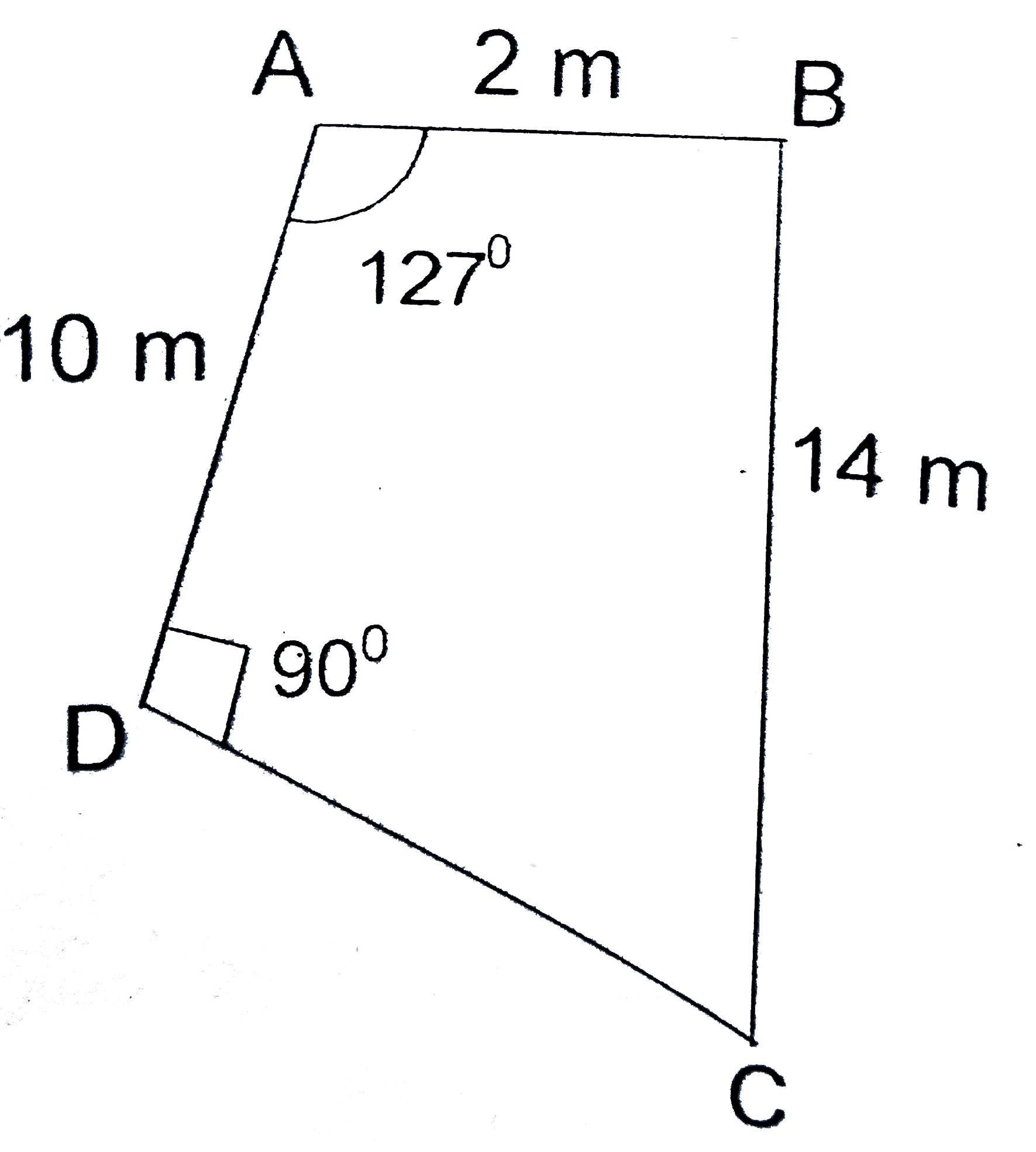 View Solution
View SolutionFor the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body a) A disc of radius a b) A ring of radius a c) A square lamina of side a d) Four identical rods forming square of side a
View SolutionMoment of inertia of an ellipse shaped wire of mass 'm', semimajor axis 'a' about an axis passing through the centre and perpendicular to the plane of wire can be :
View Solution


