A uniform disc is acted by two equal forces of magnitude F. One of them, acts tangentially to the disc, while other one is acting at the central point of the disc. The friction between disc surface and ground surface in nF. If r be the radius of the disc, then the value of n would be (in N)
0
1.2
2.0
3.2
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the uniform disc and apply the principles of rotational dynamics and translational motion.
Step 1: Identify the Forces Acting on the Disc
The disc is acted upon by two equal forces of magnitude F:
- One force F acts tangentially to the disc.
- The other force F acts at the center of the disc.
Additionally, there is a friction force f acting at the point of contact with the ground, which is given as nF.
Step 2: Establish the Equations of Motion
Let:
- A be the linear acceleration of the center of mass of the disc.
- α be the angular acceleration of the disc.
Since the point of contact with the ground has zero acceleration (it is rolling without slipping), we can relate the linear acceleration and angular acceleration as follows:
\( A = \alpha r \)
where r is the radius of the disc.
Step 3: Apply Newton's Second Law for Linear Motion
The net force acting on the disc in the horizontal direction can be expressed as:
\( 2F - f = mA \)
where m is the mass of the disc.
Step 4: Apply the Torque Equation
The torque about the center of mass due to the forces can be expressed as:
\( \tau = F \cdot r + f \cdot r = I \alpha \)
where I is the moment of inertia of the disc. The moment of inertia for a uniform disc is given by:
\( I = \frac{1}{2} m r^2 \)
Substituting the values, we have:
\( F \cdot r + f \cdot r = \frac{1}{2} m r^2 \cdot \alpha \)
Step 5: Substitute Angular Acceleration
From Step 2, we know:
\( \alpha = \frac{A}{r} \)
Substituting this into the torque equation gives:
\( F \cdot r + f \cdot r = \frac{1}{2} m r^2 \cdot \frac{A}{r} \)
This simplifies to:
\( F + f = \frac{1}{2} m A \)
Step 6: Substitute the Friction Force
Since the friction force is given as f=nF, we substitute this into the equation:
\( F + nF = \frac{1}{2} m A \)
This simplifies to:
\( (1 + n)F = \frac{1}{2} m A \)
Step 7: Equate Linear Motion and Torque Equations
From the linear motion equation, we have:
\( 2F - nF = mA \)
This can be rearranged to:
\( (2 - n)F = mA \)
Step 8: Relate the Two Equations
Now we have two equations:
1. \((1 + n)F = \frac{1}{2} m A\)
2. \((2 - n)F = mA\)
We can express A from the second equation:
\( A = \frac{(2 - n)F}{m} \)
Substituting this expression for A into the first equation gives:
\( (1 + n)F = \frac{1}{2} m \left(\frac{(2 - n)F}{m}\right) \)
This simplifies to:
\( (1 + n)F = \frac{1}{2} (2 - n)F \)
Step 9: Solve for n
Dividing both sides by F (assuming F≠0):
\( 1 + n = \frac{1}{2} (2 - n) \)
Multiplying through by 2 to eliminate the fraction:
\( 2 + 2n = 2 - n \)
Rearranging gives:
\( 3n = 0 \)
Thus:
\( n = 0 \)
Final Answer
The value of n is 0.
The disc is acted upon by two equal forces of magnitude F:
- One force F acts tangentially to the disc.
- The other force F acts at the center of the disc.
Let:
- A be the linear acceleration of the center of mass of the disc.
- α be the angular acceleration of the disc.
\( A = \alpha r \)
where r is the radius of the disc.
The net force acting on the disc in the horizontal direction can be expressed as:
\( 2F - f = mA \)
where m is the mass of the disc.
The torque about the center of mass due to the forces can be expressed as:
\( \tau = F \cdot r + f \cdot r = I \alpha \)
where I is the moment of inertia of the disc. The moment of inertia for a uniform disc is given by:
\( I = \frac{1}{2} m r^2 \)
\( F \cdot r + f \cdot r = \frac{1}{2} m r^2 \cdot \alpha \)
From Step 2, we know:
\( \alpha = \frac{A}{r} \)
Substituting this into the torque equation gives:
\( F \cdot r + f \cdot r = \frac{1}{2} m r^2 \cdot \frac{A}{r} \)
This simplifies to:
\( F + f = \frac{1}{2} m A \)
Since the friction force is given as f=nF, we substitute this into the equation:
\( F + nF = \frac{1}{2} m A \)
This simplifies to:
\( (1 + n)F = \frac{1}{2} m A \)
From the linear motion equation, we have:
\( 2F - nF = mA \)
This can be rearranged to:
\( (2 - n)F = mA \)
Now we have two equations:
1. \((1 + n)F = \frac{1}{2} m A\)
2. \((2 - n)F = mA\)
\( A = \frac{(2 - n)F}{m} \)
\( (1 + n)F = \frac{1}{2} m \left(\frac{(2 - n)F}{m}\right) \)
This simplifies to:
\( (1 + n)F = \frac{1}{2} (2 - n)F \)
Dividing both sides by F (assuming F≠0):
\( 1 + n = \frac{1}{2} (2 - n) \)
Multiplying through by 2 to eliminate the fraction:
\( 2 + 2n = 2 - n \)
Rearranging gives:
\( 3n = 0 \)
Thus:
\( n = 0 \)
The value of n is 0.
Similar Questions
Two forces of magnitude F are acting on a uniform disc kept on a horizontal rough surface as shown in the figure. Friction force by the horizontal surface on the disc is nF. Find the value of n.
 View Solution
View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 View Solution
View SolutionA disc of mass m and radius R, is placed on a smooth text service fixed surface . Point A is the geometrical centre of the disc while point B is the centre of mass of the disc . The moment of inertia of the dics about an axis through its centre of mass and perpendicular to the plane of the figure is I .A constant force F is applied to the top of the disc . The acceleration of the centre A of the disc at the instant B is below A (on the same vertical line ) will be :
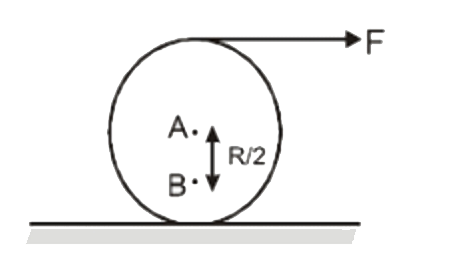 View Solution
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
 View Solution
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View SolutionA uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be regarded as uniform.
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isView SolutionStatement I: A disc is allowed to roll purely on an inclined plane as shown in Fig. A force F parallel to the incline and passing through the centre of the disc acts which remains constant during the motion.
It is possible that for certain values of F, the friction on the disc is acting along downward direction and for certain other values of F, the friction on the disc be acting along upward direction and there is no other possibility.
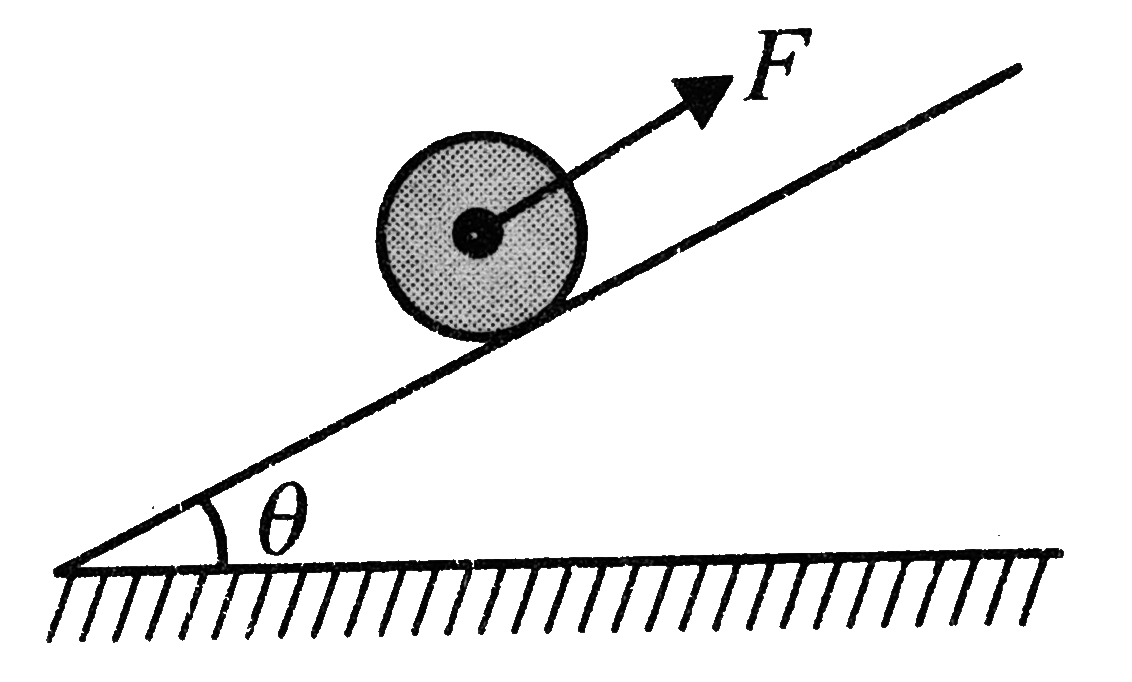
Statement II: The friction (if acting) will be static and not kinetic in nature.View SolutionThree forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
View Solution
