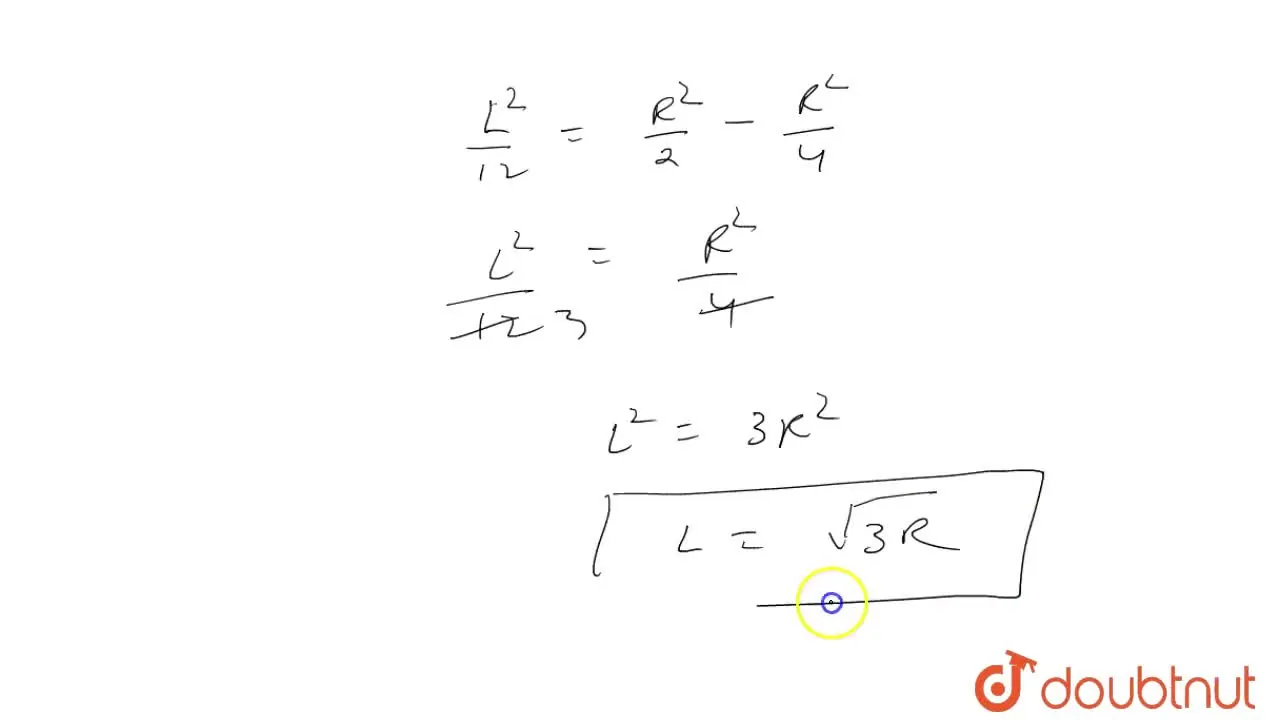
A uniform cylinder has radius R and length L. If the moment of inertia of this cylinder about an axis passing through its centre and normal to its circular face is mg equal to the moment of inertia of the same cylinder about an axis passing through its centre and normal to its length, then
Moment of inertia of cylinder about an axis passing through centre and normal circular face =MR22 Moment of inertia of cylinder about an axis passing through centre and its length =M[L212+R24]
But MR22=M[L212+R24]
R22=L212+R24⇒R44=L212,
∴L=√3R
Similar Questions
What is the moment of inertia of a hollow sphere about an axis passing through its centre ?
View SolutionThe moment of inertia of a circular ring about an axis passing through its centre and normal to its plane is 200gm×cm2 . Then moment of inertia about its diameter is
View SolutionThe moment of inertia of a circular disc about an axis passing through its centre and normal to its plane is 50 kg - m2. Then its moment of inertia about a diameter is
View SolutionThe moment of inertia of a sphere of radius R about an axis passing through its centre is proportional to-
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View Solution