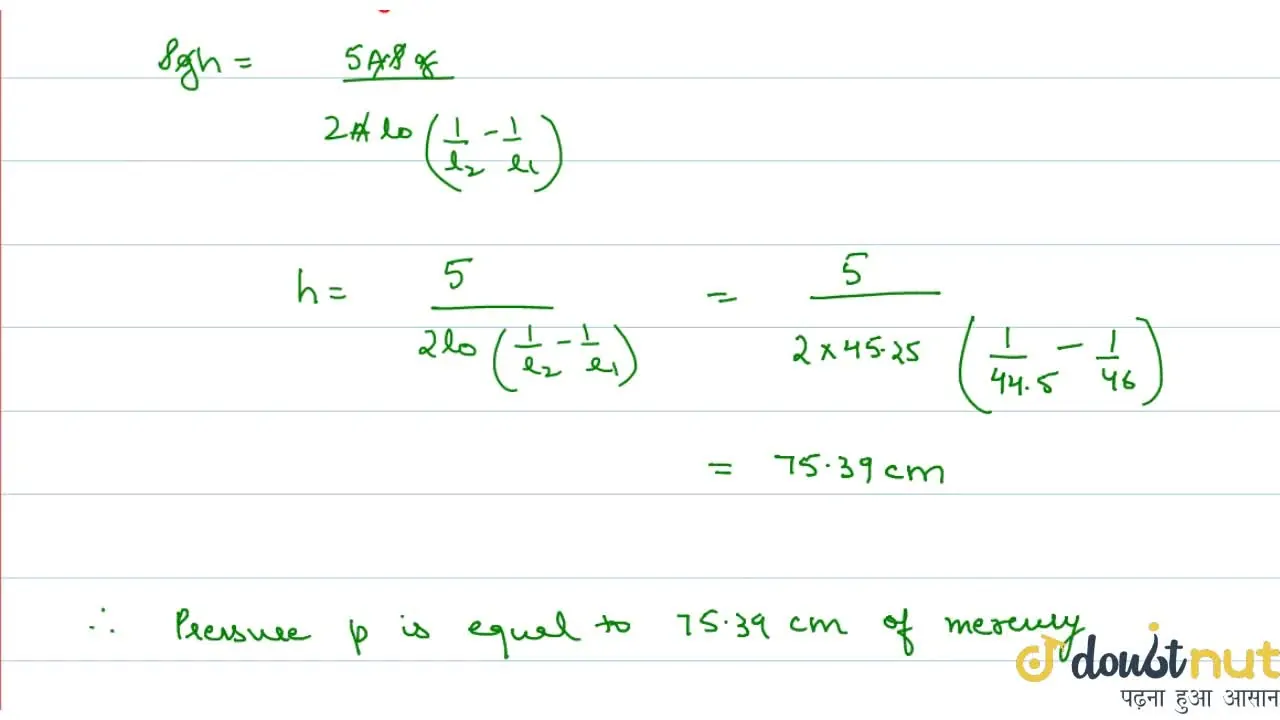A thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. when the tube is held at and angle of 60∘ with the vertical, the length of the air column above and belw the mercury pellet are 46cm and 44.5cm respectively. Calculate the ressure - in centimeters of mercury, The timperature of the system is kept at 30∘C.
When the tube is kept inclined to the vertical, the length if the upper part isl1=46cm and that of the lower part is l2=44.5cm. When the tube lies horizontally, the length on each side is
l0=l1+l22=46cm+44.5cm2=45.25cm.
Letp1andp2be the pressures in the upper and the lower parts when the tube is kept inclined, As the temperature is constant throughout, we can apply Boyle's law. For the upper part,
p1l1A=pl0A
or, p_(1)=(pl_(0))/(l_(1))...(i)
Similarly, for the lower part,
p2=pl0l2 ...(ii)
Now consider the eqilibrium of the mercury pellet when the tube is kept in inclined pisition, Let m be the mass of the mercury. The forces along the length of the tube are
(a) p1A down the tube
(b) p2up the tube
and (c) mg cos 60∘ down the tube.
Thus ,p2=p1+mgAcos60∘.
Putting from (i) and (ii),<br>(pl_(0))/(l_(2))=(pl_(0))/(l_(1))+(mg)/(2A)<br>or,pl_(0)((1)/(l_(2))-(1)/(l_(1)))=(mg)/(2A)<br>or, p=(mg)/((2Al_(0))((1)/(l_(2))-(1)/l_(1))<br>Ifthepressurepisequal→aheighthifmercury,<br>p=hrhog.<br>also, m=(5cm)Arho<br>so that hrhog=((5cm)Arhog)/(2Al_(0)((1)/(l_(2))-(1)/(l_(1)))<br>or,h=(5cm)/(2(45.25cm)((1)/(44.5cm)-(1)/(46cm))<br>'=75.39cm.
The pressure p is equal to 75.39cm of mercury.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_imagesHCV_VOL2_C24_S01_017_S01.pngwh=80%mx-autosty≤=background:white;>
Related Playlists
- BOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Short Answer14videos
KINETIC THEORY OF GASES
- BOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 117videos
KINETIC THEORY OF GASES
- BOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercises62videos
KINETIC THEORY OF GASES
- BOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises19videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer15videos
LAWS OF THERMODYNAMICS
Similar Questions
A thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally. The middle 5 cm containing Hg and the two equal parts containing air at the pressure P0.When the tube is held at an angle 60∘ with the vertical, the length of air column above and below the mercury are 46 and 44.5 cm respectively. Calculate the pressure P0 in cm of Hg (the temperature of the system is kept at 30∘C).
View SolutionA thin tube, sealed at both ends, is 100cm long. If lies horizontally, the middle 10cm containing mercury and the two equal containing air at stan-dard atmospheric pressure. If the tube is now turned to a verical position, by what amount will the mercury be displaced ?
View SolutionA glass tube sealed at both ends is 100cm long, It lies horizontally with the middle 10cm containing mercury. The two ends of the tube contain air at 27∘Cand at a pressure 76cm of mercury. The air column on one side is maintained at 0∘Cand the other side is maintained at 127∘C. Calculate the length of the air column on the cooler side. neglect the changes in the volume of mercury and of the glass.
View Solution
If above tube is held vertical with open end upward then find the length of air column (in cm).View SolutionIn the given figure a glass tube lies horizontally with the middle 20cm containing mercury. The two ends of the tube contains air at 27∘C and at a pressure 76cm of mercuy. Now the air column on one side in maintained at 0∘C and the other side is maintained at 127∘C. Find the new length of the air column on the cooler side. Neglect the changes in the volume of mercury and of the glass.
 View Solution
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionAglass tube scaled at both end is 1m long. It lies horizontally with middle 10cm containing Hg. The two ends of the tube, eqaul in length, contain air at 27∘C Neglect the chang in length of Hg column. Then the change in length on two sides is
View SolutionA mercury barometer reads 75cm in vertical position . If the tube is inclined by 60∘ to the vertical, the length of the mercury in the tube will be
View SolutionWhat will be the length of mercury column in a barometer tube when the atmosperic pressure is 75cm of mercury and the tube is inclined at an angle of 60∘ with the horizontal direction?
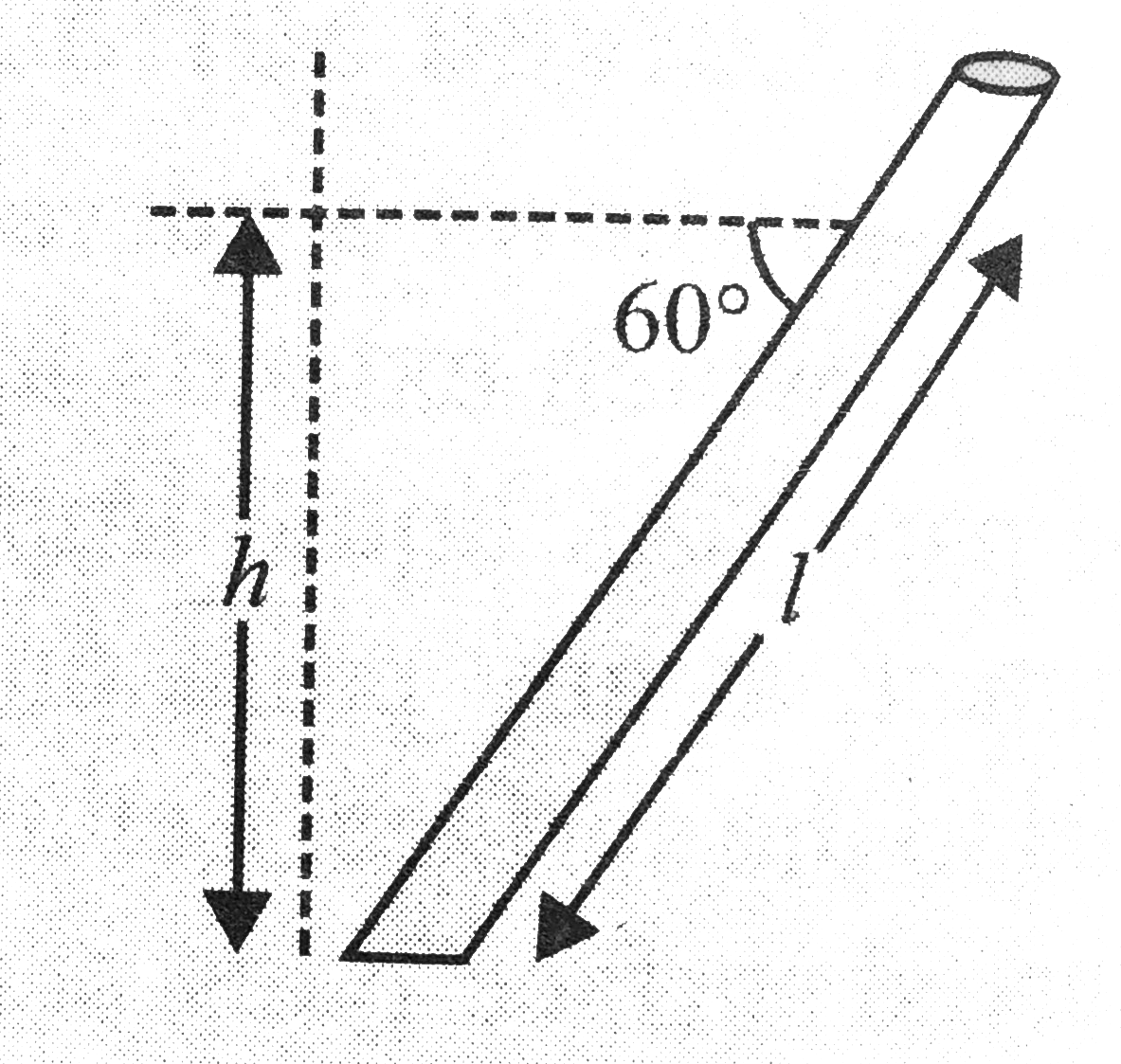 View Solution
View Solution