A string 120cm in length sustains a standing wave with the points of the string aat which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
When astring fixed at both the ensds sustains a standing wave , there are n (a whole number) segments of the length of the string , where particles in each segment of the string oscillate in phase with each other and are out of phase with the particles of the adjacent segment , the string contain n loops between its ends . Under this condition the amplitude of the oscillation varies from the point to point on the string as a harmonic function ( a sine function or a cosine function ). A typical equation for the standing wave can be given as y=ymaxsinkxcosωt.
Let the string be lying along the x - axis between x=0 and x=120cm. Let the amplitude variation along the length of the string be given by a=amaxsinkx , where k is the propagation constant.
First Method : (k=ωv=2πλ)
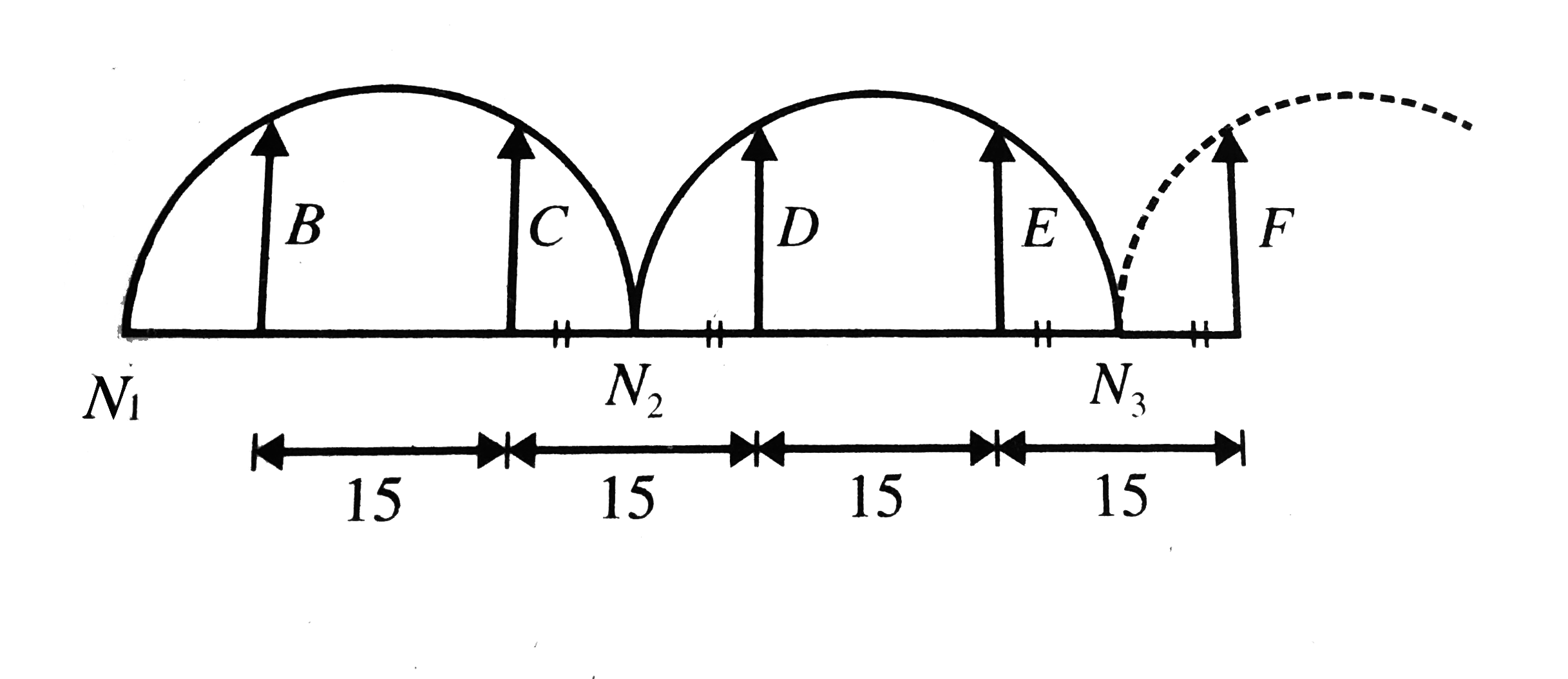
Let the string be oscillating in its nth harmonic . The string will constant n loops with end points as node . The points in a loop , where the displacement amplitudes are 3.5mm will be located symmetrically about antinode , as shown in the Fig . 7.37.
Now BC=DE=...=15cmandCD=EF=...=15cmcm ( A sine function given by y=sinx(0≤x≤π) is symmetrical about x=π/2, etc.)
CD=CN2+N2D
=(1202n−7.5)+(1202n−7.5)=2(1202n−7.5)
THus , 2(1202n−7.5)=15orn=4
The oscillations corresponds to the 4th harmonic ( the 3rd overtone ). The atring will oscillate in 4 loops . There are a total of 5 nodes ( including the nodes on the end of the next node the distance is λ/2 , the length of the string l=4λ/2 .
or λ/2=l/4=30cmorλ=60cm
k=2πλ=π30
Amplitude as function of x is
a=amaxsinkx=amaxsin(πx30)
Now at x=7.5,12.5cm,a=3.5mm
or 3.5=amaxsin(7.5π30)
or 3.5=amaxsin(π)4=amax√2
amax=3.5√2=4.935=5mm
Second Method : Suppose that the points shown in Fig . 7.38 represent the points which have equal amplitudes and are equally spaces . Now , distance two consecutives nodes is λ/2 . Therefore ,
a+b+c=λ/2 (i)
From symmetry considerations
a=c=d (ii)
Now , for such points to be equidistant throughout the string ,
b=c+d (iii)
From Eqs. (ii) and (iii),
b=2a
From Eq. (i) , we get
a+2a+a=λ/2
or a=λ/8 (iv)
b=2a=λ/4. The points where displacement amplitudes are 3.5mm are λ/4 apart.
∴λ/4=15orλ=60cm
Hence , a=λ/8=7.5cm
[ Note that only one value for b , i.e., distance between to such consecutive points exist , hence only one such set of points exist on the string and such points are λ/4 apart ]
No. of loops =2Lλ=2×12060=4
The string is in the 4th harmonic or 3rd overtone .

Similar Questions
A string 120cm in length sustains a standing wave, with the points of the string at which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude. To which overtone do these oscillations correspond ?
View SolutionA string 120cm in length sustains a standing wave with the points of the string aat which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
View SolutionA stretched string of length 200cm supports a stationary wave with points having a displacement amplitude of mm being separated by equal intervals of 20cm. To which overtone do these vibrations belong.
 View Solution
View SolutionA string of mass 0.2 kg/m and length l= 0.6 m is fixed at both ends and stretched such that it has a tension of 80 N. the string vibrates in 3 segments with maximum amplitude of 0.5 cm. the maximum transverse velocity amplitude is
View SolutionA standing wave is created on a string of length 120m and it is vibrating in 6th harmonic. Maximum possible amplitude of any particle is 10cm and maximum possible velocity will be 10cm/s. Choose the correct statement.
View SolutionA wave travelling on a string at a speed of 10ms−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave ? (b) If the displacement of a particle is 1.5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant ?
View SolutionA harmonic wave is travelling on a stretched string . At any particular instant , the smallest distance between two particles having same displacement , equal to half of amplitude is 8cm. Find the smallest separation between two particles which have same values of displacement (magnitude only) equal to half of amplitude.
View SolutionA series of pulses, each of amplitude 0.150m, are sent on a string that is attached to a wall at one end. The pulses are reflected at the wall and travel back along the string without loss of amplitude. When two waves are present on the same string. The net displacement of a given point is the sum of the displacement of the individuals waves at the point. What is the net displacement at point on the spring where two pulses am crossing, (a) if the string is rigidly attached to the post? (b) if the end at which reflection occurs is free is slide up and down ?
View SolutionA strain of sound waves is propagated along an organ pipe and gets reflected from an open end . If the displacement amplitude of the waves (incident and reflected) are 0.002cm , the frequency is 1000Hz and wavelength is 40cm. Then , the displacement amplitude of vibration at a point at distance 10cm from the open end , inside the pipe is
View SolutionTwo travelling waves of equal amplitudes and equal frequencies move in opposite direction along a string . They interfere to produce a standing wave having the equation .
y=Acoskxsinωt
in which A=1.0mm,k=1.57cm−1andω=78.5s−1. (a) Find the velocity and amplitude of the component travelling waves . (b) Find the node closest to the origin in the region x>0. ( c) Find the antinode closest to the origin in the region x>0 . (d) Find the amplitude of the particle at x=2.33cm.View Solution


