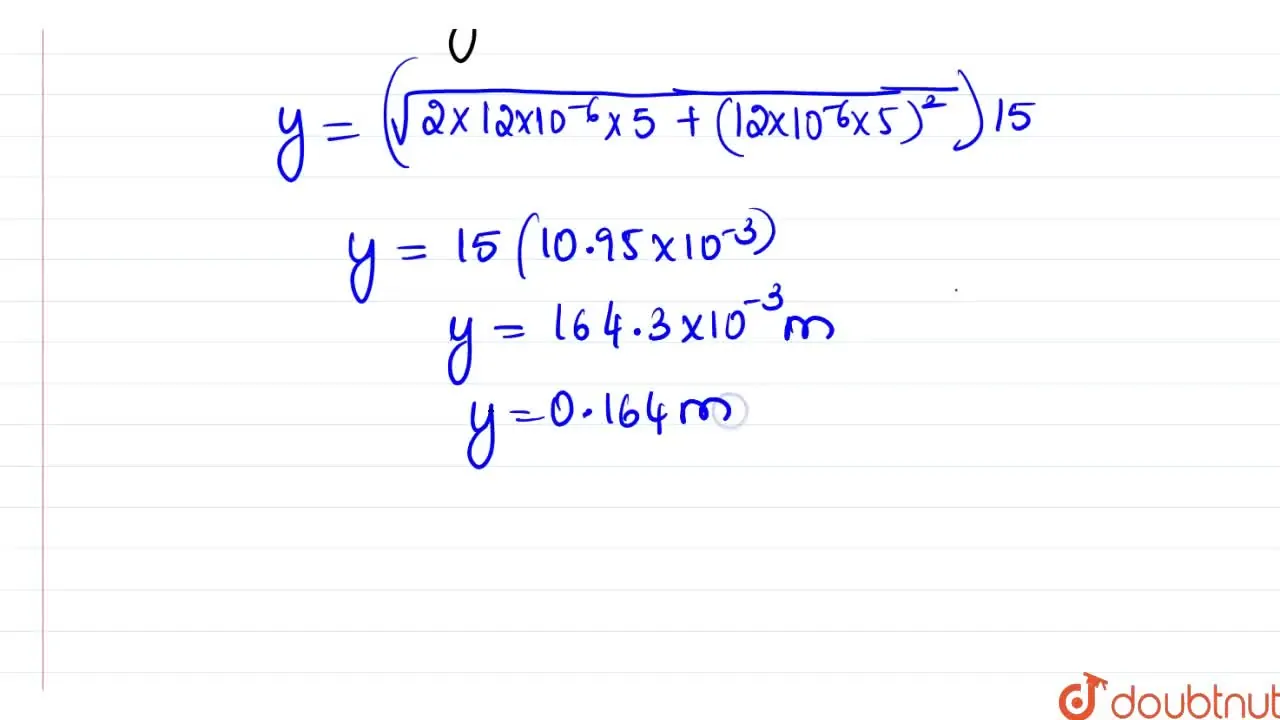A steel rail 30 m long is firmly attached to the roadbed only at its ends. The sun raises the temperature of the rail by 5∘C, causing the rail to buckle. Assuming that the buckled rail consists of two straight parts meeting in the centre, calculate how much the centre of the rail rises. coefficient of linear expansion of steel is 12×10−6/K.

As indicated in Fig. we let the initial length be 2 s and the final total length be 2(s+Δs)
The height of the centre of the buckled rail is denoted by y. Assuming that the standard coefficient α of linear expansion can be used (in spite of the fact that the ends are anchored), we have Δs=αsΔT.
By the Pythagorean theorem
y=√(s+Δs)2−s2=√2sΔs+(Δs)2
√2αΔT+(αΔT)2
With s=15.0m,α12×106K, and ΔT=50K, we obtain
y=(15.0m)√(12×10−4)+(6×10−4)2=0.52m
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.123videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.222videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5C−1.
View SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5∘C−1.
View SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5∘C−1.
View SolutionA steel beam used in the construction of a bridge has a length of 30.0 m when the temperature is 15∘C. On a very hot day, when the temperature is 35∘C, what will the beam's change in length be? (The coefficient of linear expansion for structural steel is +1.2×10−5/∘C.)
View SolutionA steel wire 2mm in diameter is just stretched between two rigid walls at 20°C. If the temperature falls to 10°C, find the tension in the wire. Linear coefficient of expansion of steel = 11×10−6/kandY=2×1011N/m2
View SolutionA steel rod is rigidly clamped at its two ends. The rod is under zero tension at 20∘C. If the temperature rises to 100∘C, what force will the rod exert on one of the clapms? Area of cross section of the rod =2.00mm2 . Coefficient of linear expansion of steel =12.0×10−6C−1 and Young's modulus of steel 2.00×1011Nm−2.
View SolutionTwo rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20∘C, the length of the copper rod is 0.5 m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's moulus of steel. (The coefficient of linear expansion of copper, αc=1.6×10−5∘C and Young's modulus of copper is 1.3×1013N/m2).
View SolutionThe ends Q and R of two thin wires, PQ and RS, are soldered (joined) together. Initially each of the of wire has a length of 1m at 10∘C. Now the end P is maintained at 10∘C, while the ends S is heated and maintained at 400∘C. The system is thermally insultated from its surroundings. If the thermal conductivity of wire PQ is twice that of the wire RS and the coefficient of linear thermal expansion of PQ is 1.2×10−5K−1, the change in length of the wire PQ is
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composite rod increases by 1.91mm. When the composite rod is prevented from expanding by holding it between two rigid walls, it is found that the constituent rods have remained unchanged in length inspite of rise of temperature. Find young's modulus and the coefficient of linear expansion of the second rod (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionA wire is made by attaching two segments together end to end. One segment is made of aluminium and the other is steel. The effective coefficient of linear expansion of the two segment wire is 19×10−6/∘C. The fraction length of aluminium is (linear coefficient of thermal expansion of aluminium and steel are 23×10−6.∘C and 12×10−6/∘C,
View Solution