A steel flywheel is made in the shape of a solid ring of 40 cm external and 30 cm internal diameter. What is its maximum design speed? At what speed will it fly apart?
The correct Answer is:3700 r.p.m ; 7500 r.p.m
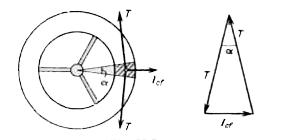
We shall solve the problem in a rotating reference frame. Consider a segment of the flywheel which subtends small angle α at its centre (Fig.). The forces acting on this metallic segment are the centrifugal force of inertia and two elastic forces. The relation between them follows from the condition for equilibrium: Ict=Tα. Here T=σS, where S is the cross-sectional area of the flywheel rim, and α is the stress. The volume of the separated segment is V=lS=αSRav, where Rav=(R+r)/2 is the average radius of the flywheel rim. The centrifugal force of inertia is
Ict=mω2Rav=ω2Ravρv=αρSω2R2av
where ρ is the density of the metal. Substituting into the condition for equilibrium, we obtain the dependence of the stress in the metal on the speed of rotation:
σ=ρω2R2av
The speed is safe when the stress does not exceed the elastic limit. In this case the elastic forces will return the flywheel to its original state when the speed of rotation is reduced. Therefore the maximum safe speed of rotation of the flywheel is
ω=√σEρR2av=2R+r√σEρ
The flywheel will fly apart when the stress in it reaches the breaking stress, i.e. when
ωbr=2R+r√σtwρ
Similar Questions
The inner and outer diameter of a ring is 14 cm and 28 cm respectively. What is the area of ring?
View SolutionA piece of wire is bent in the shape of an equilateral triangle of each side 6.6 cm. It is re-bent to form a circular ring. What is the diameter of the ring?
View SolutionA piece of wire is bent in the shape of an equilateral triangle of each side 6.6 cm. It is re-bent to form a circular ring. What is the diameter of the ring?
View SolutionAt what speed will the velocity head of stream of water be 40 cm?
View SolutionIf the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm then its slant height is
View SolutionA garden hose with an internal diameter of 1.9 cm is connected to a (stationary) lawn sprinkler that consists merely of a container with 20 holes, each 0.15 cm in diameter. If the water in the hose has a speed of 0.91 m/s, at what speed does it leave the sprinkler holes?
View SolutionWhat is the volume (in cm)2 of a spherical shell with 8 cm and 10 cm as its internal and external diameters respectively ?
View SolutionWater flows through a pipe of diameter 8.0 cm with a speed of 10.0 m/s . It then enters a smaller pipe of diameter 3.0 cm . What is the speed of the water as it flows through the smaller pipe ?
View SolutionA hollow sphere of external and internal diameters 6 cm and 4 cm respectively is melted into a cone of base diameter 8 cm. What is the height of the cone?
View SolutionA cylinder 84 cm long is made of steel. Its external and internal diameters are 10 cm and 8 cm respectively. What is the volume of the steel in the cylinder (in 10−3m3 and correct up to three decimalplaces) ?
View Solution

