A steel cable is made up of 120 wires each of 1 mm diameter.The rope's length is 4 m, the distance between the suspension points is 3.8 m (Fig.). A weight of 1 tonne mass is suspended in the middle of the rope. What will be the rope's elongation? What weight will cause the rupture of the rope? The rope is made of soft steel.
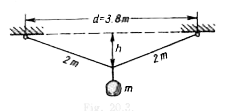
The correct Answer is:3.3 mm ; 2.4 tonnes
The sag in the cable is h=√(l/2)2−(d/2)3=0.625m. The force extending the cable is F=mgl/4h=1.57×104N, the crosssectional area of the cable is 120πD2/4=30πD2=9.4×10−5m2. Hence applying Hooke.s law we find the extension of each section of the cable:
Δl−FlES=mgl24ESh
The force capable of rupturing the cable is found from the breaking stress : Fm=σmS. The load capable of rupturing the cable is M=4σmSh/gl.
Similar Questions
IF the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionIf the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View Solution
Knowledge Check
- Question 1 - Select One
A rope of length 10 m has been divided into 8 pieces of the same length. What is the length of each piece ?
A2 m 25 cmB1 m 35 cmC1 m 55 cmD1 m 25 cm - Question 2 - Select One
Sonia made two concentric circles with two pieces of rope. The distance between two circles is 6 cm. What is difference between lengths of 2 ropes used to make circles ?
A12 cmB12π cmC36 cmD36π cm - Question 3 - Select One
A mass of 20 kg is suspended by a rope of length 4 m from the ceiling. A force of 60 N is applied at the midpoint of the rope in the horizontal direction. What is the angle made by the rope with the vertical in equilibrium? Assume that the mass of the rope is negligible and g=10m/s2
Aθ=tan−1(110)Bθ=tan−1(15)Cθ=tan−1(310)Dθ=tan−1(12)
A rope of length 10 m has been divided into 8 pieces of the same length. What is the length of each piece?
View SolutionA heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is 1. Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log.
View SolutionA rope of length of 2m is tied between two ends . If the speed of transverse waves propagating in the rope is 4ms−1 and the tension in the rope is 2 N , find the mass of the rope is C.G.S units .
View SolutionA cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope when the cat move upwards with in acceleration a=2m/s2 relative to the rope ?
 View Solution
View SolutionA mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
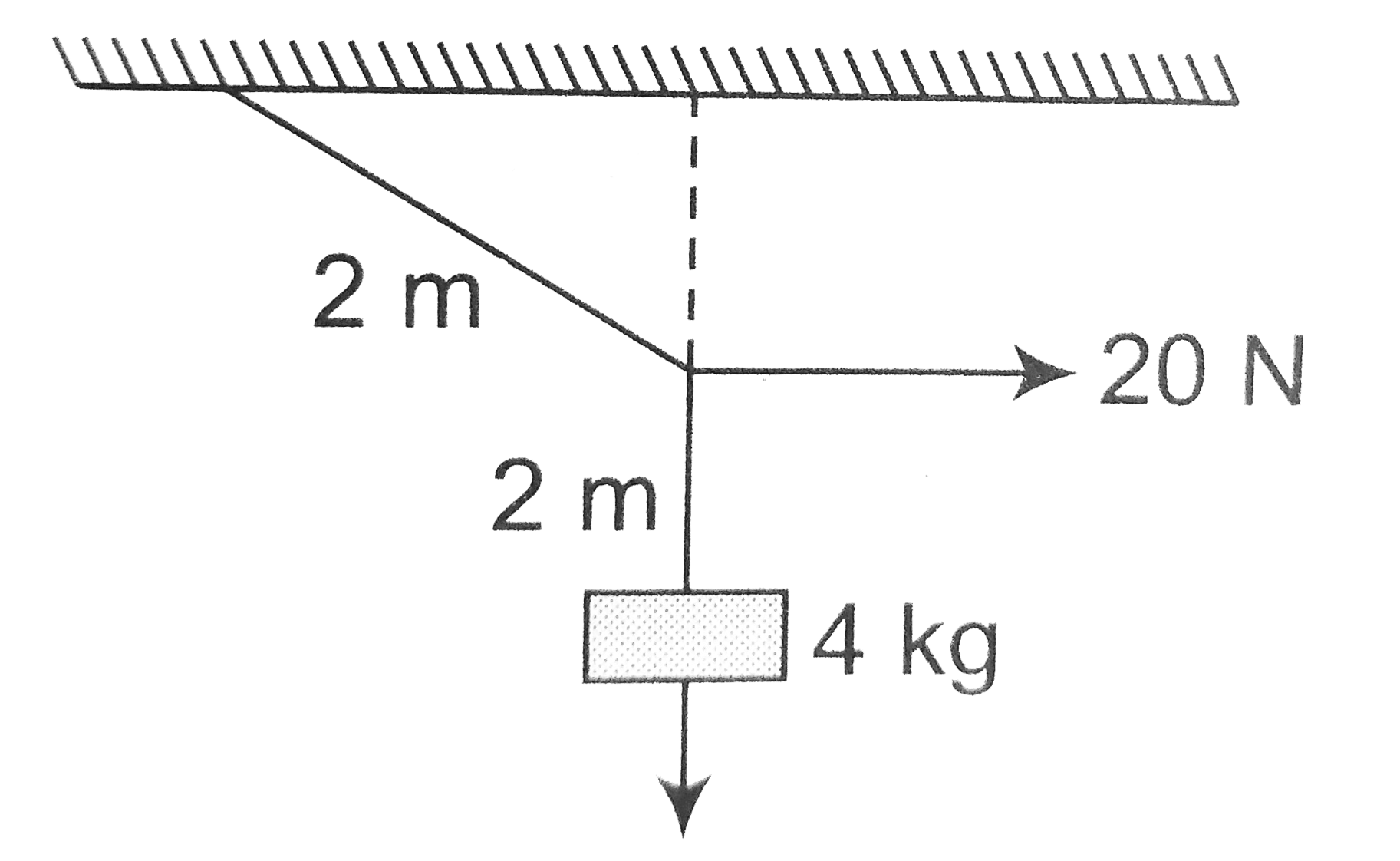 View Solution
View Solution
