A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
Let at any instant, the boby is at angular position θ with respect to the vertical line drow from the center of mirror , if ϕ is the angular displacement of the ball about its senter, then

Restoring tarque acting on the ball τ=−mgsinθ×r
For small θ,sinθ ∴τ=−mgsinθ×r
or τ=−mg[rR−r]ϕr=mg(r2R−r)(−ϕ)
Angular acceleration α=mgl(r2)R−r)(−ϕ)
Now comparing above equation with atandard eqation of SHM, α=−ω2ϕ,we≥tω=√mgl(r2R−r)
Here l is moment of inertia of the rolling ball about the point of constant which is l=7/5mr2
⎷mg75mr2(r2R−r)=√57g(R−r)
and T=2πω=2π√7(R−r)5g
Alternate method: We can that when the CM of the boby is shifted slightly by an angle θ relative to the center of curvature of the surface, the magnitude of acceleration of the CM of the boby can be given as
a=gsinθ1+k2r2
(because the body is accelerating down the inclined plane of instancous angle θ)
Subastituting sinθ=θ=xR−r , we have
a=−gx(R−r)(1+k2r2)
(negative sign is given because ¯a and ¯x are oppositely directed)
Comparing the above equation with a=−ω2x, we have
ω=
⎷g(R−r)(1+k2r2)
For solid sphere k2=2/5r2.
Hence ω=√57g(R−r)

Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.223videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.
 View Solution
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA spherical shell of mass m and radius R is rolling up without slipping on a rough inclined plane as shown in the figure. The direction of static friction acting on the shell is
View Solution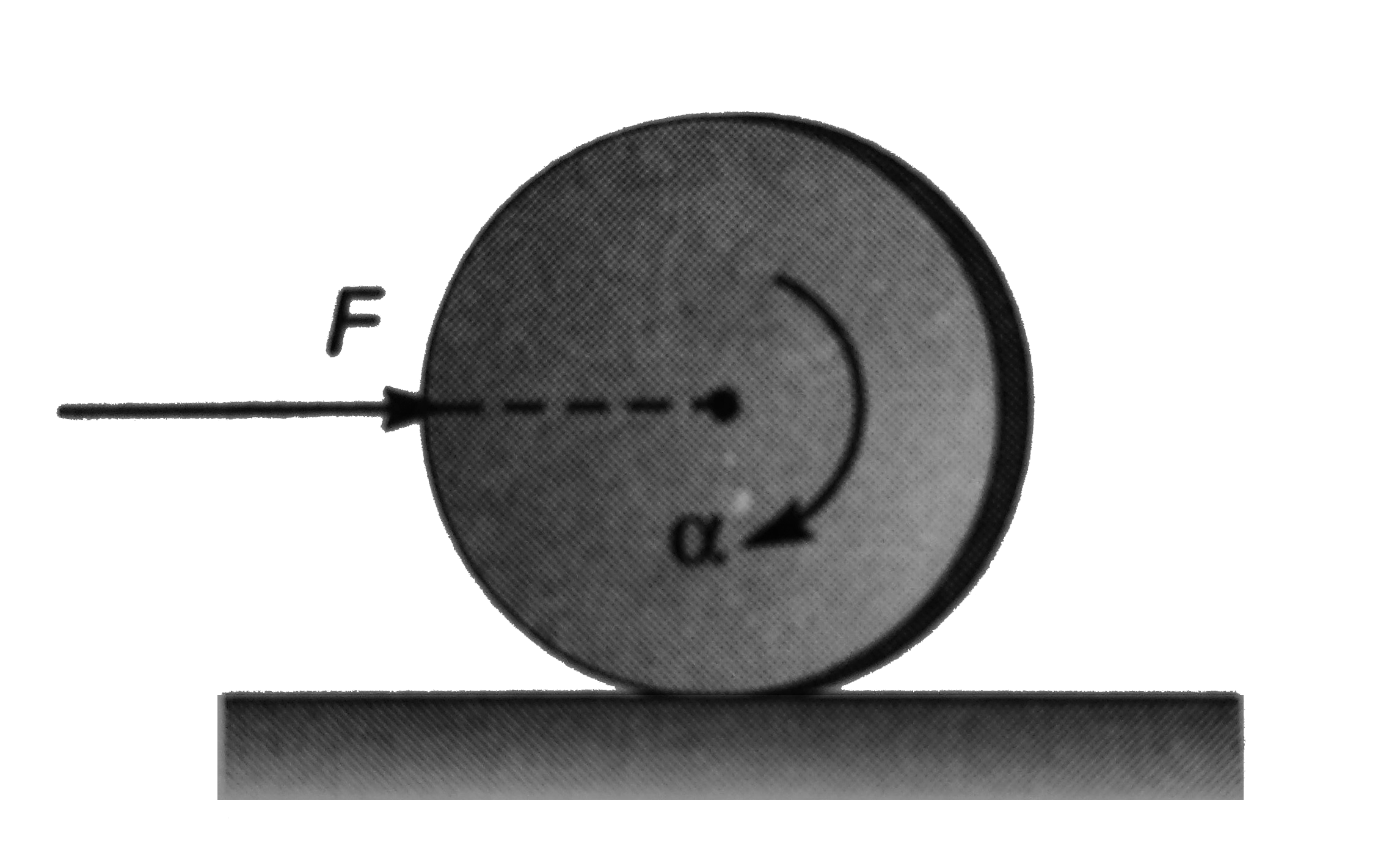
Consider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. Angular momentum of the disc will be conserved aboutView SolutionConsider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The work done by the frictional force at the instant of pure rolling is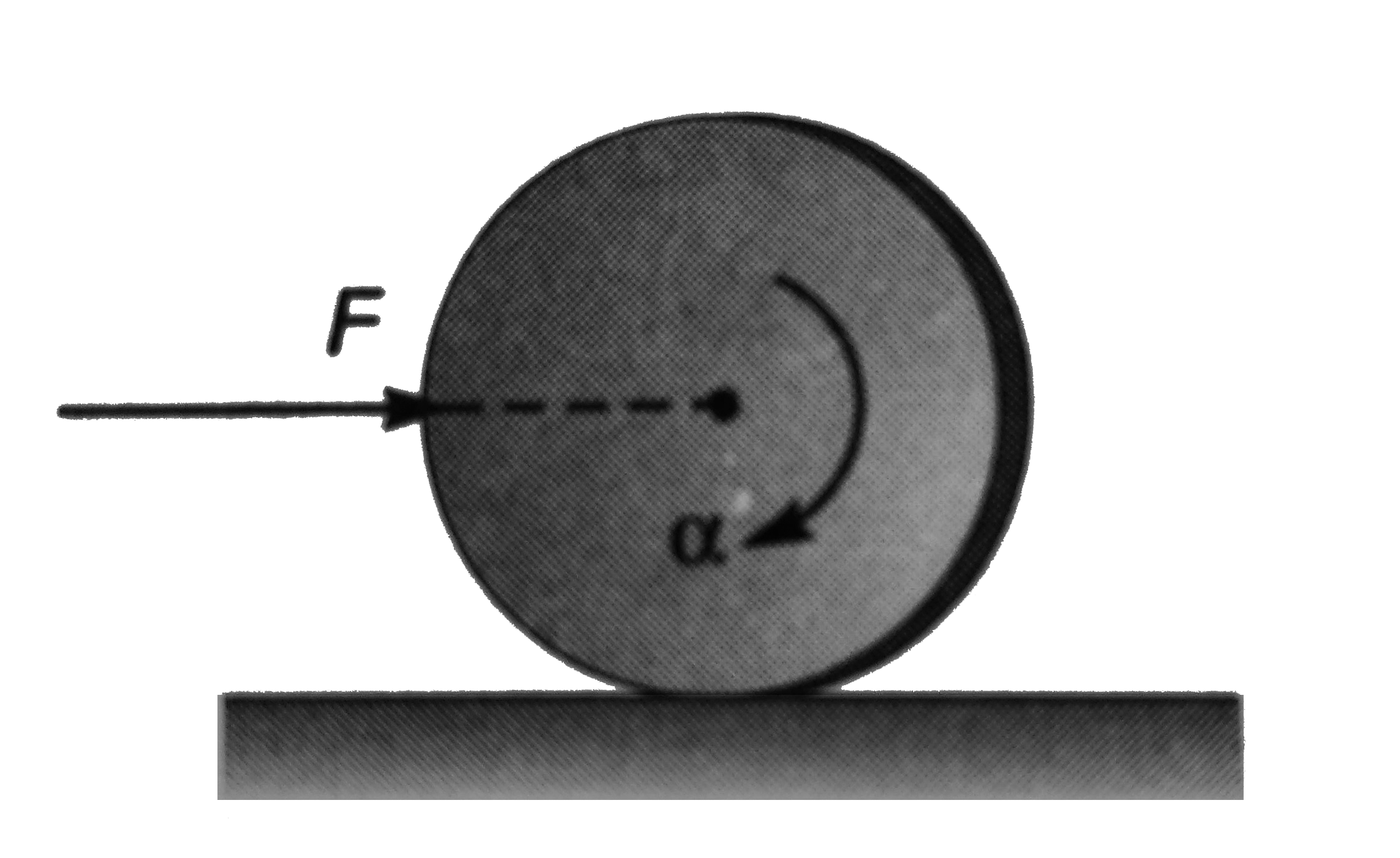 View Solution
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.
 View Solution
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.
 View Solution
View SolutionA uniform thin spherical shell of mass m and radius R rolls down without slipping over an inclined plane of angle θ with the horizontal. The ratio of rotational kinetic energy to the total kinetic energy of the shell will be
View SolutionA spherical metal ball of mass m and radius (r) is falling through a viscous medium. The value of its terminal velocity is proportional to
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.View Solution


