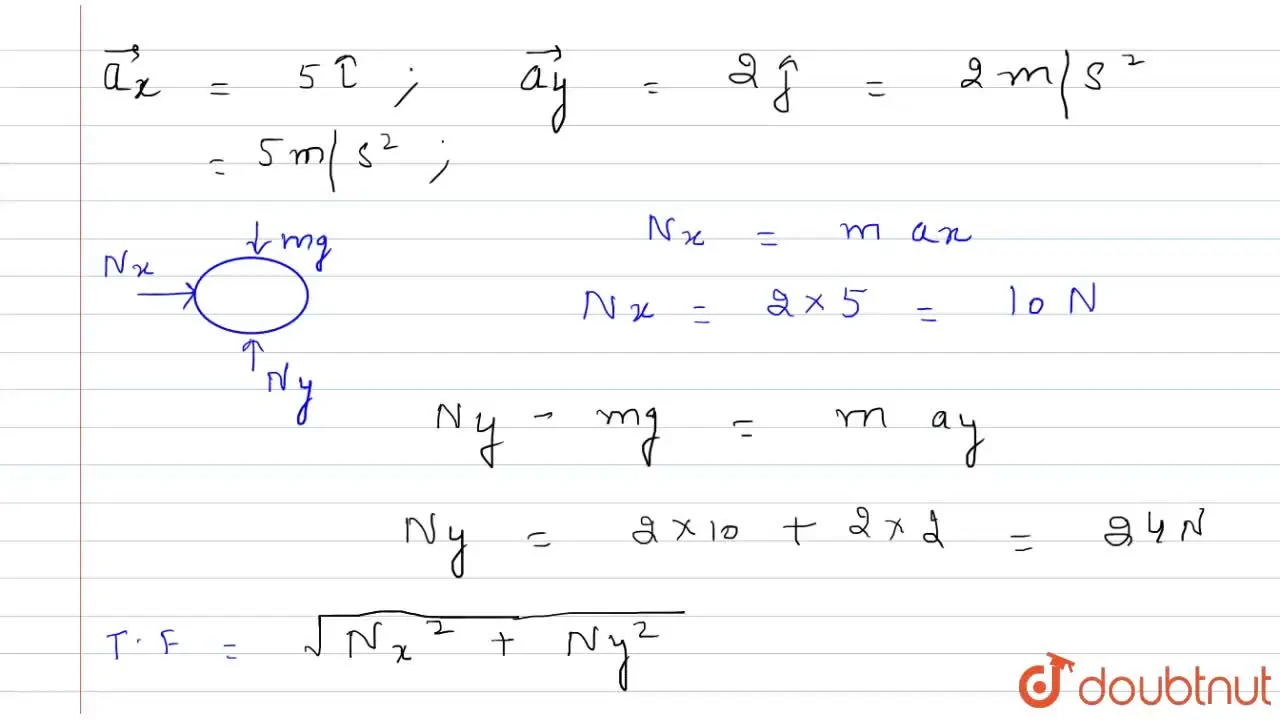A solid sphere of mass 2 kg is resting inside a cube as shown in fig. The cube is moving with a velocity →v=(5tˆi+2tˆj)ms−1. Here t is time in seconds. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube?

The velocity of the sphere is same as that of the cube, which is given as →v=5tˆi+2tˆj.
Hence, acceleration of the sphere: →a=d→vdt
or →a=(5ˆi−2ˆj)ms−2
Hence, ax=5ms−2 and ay=2ms−2
From FBD of sphere Nx=max=2×5=10N
Ny−mg=may⇒Ny=2×10+2×2=24N
Total force =√N2x+N2y=√(10)2+(24)2=26N.

Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A solid block of mass 2kg is resting inside a cube shown in figure The cube is moving with a velocity ˆv=5ˆi+2ˆjms−1 If the coefficient of friction between the surface of cube and block is 0.2 then the force of friction between the block and cube is
 View Solution
View SolutionA sphere of mass 1kg rests at one corner of a cube. The cube is moved with a velocity v=(8tˆi−2t2)ˆj, where tis time in second . The force by sphere on the cube at t=1s is (g=10m/s−2) [figure shown vertical plane of the cube]
 View Solution
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionA small sphere of mass 1 kg is moving with a velocity (6ˆi+ˆj)ms−1. It hits a fixed smooth wall and rebound with velocity (4ˆi+ˆj)ms−1. The coefficient of restitution between the sphere and the wall is
View SolutionAn object of mass 2 kg at rest at origin starts moving under the action of a force
→F=(3t2ˆi+4tˆj)N The velocity of the object at t = 2 s will be -View SolutionA body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=(6ˆi−12ˆj)ms−1, the time at which it will just have a velocity along the y-axis is :
View SolutionIn a particular crash test, a car of mass 1500 kg collies with a wall as shown in fig. The initial and final velocities on the car are →vi=−15.0ˆims−1 and →vf=5.00ˆims−1, respectively. If the collision lasts 0.150s, find the impulse caused by the collision and the average force exerted on the car.
 View Solution
View SolutionA body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=6ˆi−12ˆjms−1, the time at which it will just have a velocity along the y-axis is :
View SolutionA body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=6ˆi−12ˆjms−1, the time at which it will just have a velocity along the y-axis is :
View SolutionA body of mass 5 kg statrs from the origin with an initial velocity →u=(30ˆi+40ˆj)ms−1. If a constant force (−6ˆi−5ˆj)N acts on the body, the time in which the y component of the velocity becomes zero is
View Solution