A solid cylinder of radius r and mass m is placed with no initial velocity on a moving belt 'B'. It is placed against a rough wall ’A', which restricts the sliding of the cylinder on the belt as shown in the figure. Assuming that the
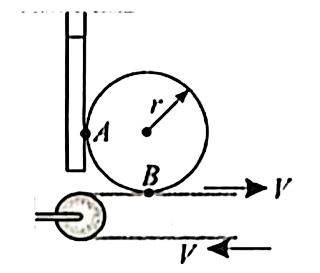
coefficient of friction at A and B is μ(<1), the angular acceleration of the cylinder will be
gr(μ1+μ)
2gr(μ1+μ)
g2r(μ1+μ)
gr(μ2+μ)
The correct Answer is:B
For linear motion, apply newton.s laws
N1−μN=0μ1=μN ......(i)
μN1+mg=N.......(ii)
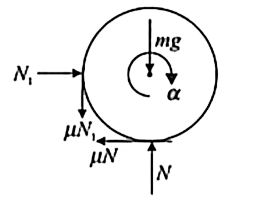
For rotation motion.
(μN−μN1)∙r=(mr22α)
μmg1−μ2−μ2mg1−μ2=mr2α⇒α=2μgr(1+μ)
Related Playlists
Similar Questions
A force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
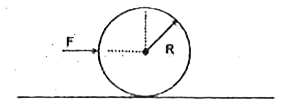 View Solution
View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
 View Solution
View SolutionA solid cylinder of mass m is wrapped with an inextensible light string and, is placed on a rough inclined plane as shown in the figure. The frictional force acting between the cylinder and the inclined plane is :
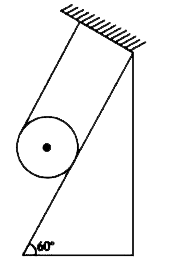 [The coefficient of static friction, μs is 0.4]View Solution
[The coefficient of static friction, μs is 0.4]View SolutionA uniform circular cylinder of mass m and radius r is given an initial angular velocity ω and no initial translational velocity it is placed in contact with a plane inclined at an angle α to the horizontal. If there is a coefficient of friction μ for sliding between the cylinder and plane. Find the distance the cylinder moves up before sliding stops also calculate the maximum distance it travels up the plane assume μ>tanα.
View SolutionA uniform circular cylinder of mass m and radius r is given an initial angular velocity ω and no initial translational velocity it is placed in contact with a plane inclined at an angle α to the horizontal. If there is a coefficient of friction μ for sliding between the cylinder and plane. Find the distance the cylinder moves up before sliding stops also calculate the maximum distance it travels up the plane assume μ>tanα.
View SolutionA plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
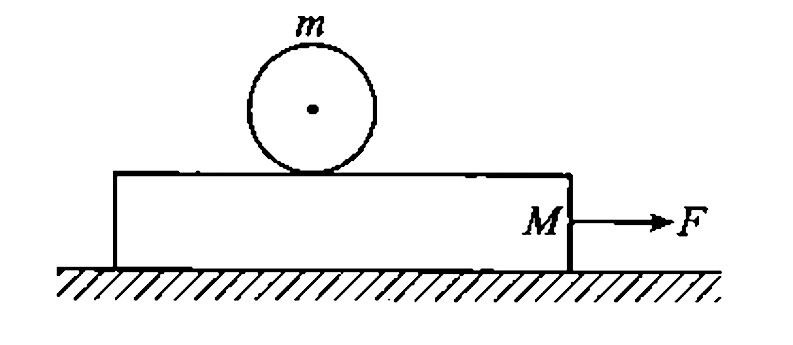 View Solution
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionA solid cylinder is given a velocity v0 and an angular speed ω0 in the anticlockwise direction and then it is placed gently on a very long rough plank ( initially at rest ) as shown in the figure. Then, choose the incorrect statement :
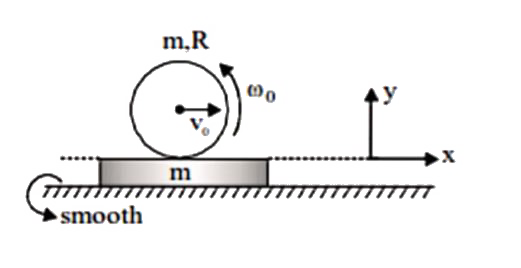 View Solution
View Solution

