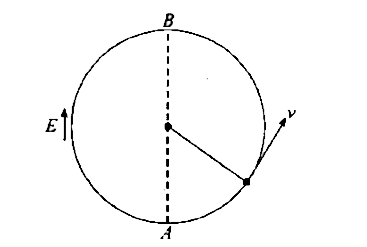
A small sphere of mass m=0.5kg carrying a positive charge q=110μC is connected with a light, flexible, and inextensible string of length of length r=60cm and whirled in a vertical circle. If a vertically upward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
To solve the problem step by step, we will follow the reasoning laid out in the video transcript while ensuring clarity in each step:
Step 1: Identify Given Values
We have the following values provided in the problem:
- Mass of the sphere, m=0.5kg
- Charge of the sphere, q=110μC=110×10−6C
- Length of the string (radius of the circle), r=60cm=0.6m
- Electric field strength, E=105N/C
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate Forces at the Highest Point
At the highest point of the circle, the forces acting on the sphere are:
1. Weight of the sphere, W=mg=0.5×10=5N (acting downward)
2. Electric force due to the electric field, Fe=qE=(110×10−6)×(105)=11N (acting upward)
Step 3: Determine the Net Force Required for Circular Motion
At the highest point, for the sphere to just complete the circle, the centripetal force required is provided by the net force acting on it. The net force Fnet at the highest point can be expressed as:
Fnet=Fe−W
Substituting the values:
Fnet=11N−5N=6N
Step 4: Relate Net Force to Centripetal Force
The net force acting on the sphere at the highest point provides the necessary centripetal force for circular motion:
mv2r=Fnet
Substituting the known values:
0.5v20.6=6
Step 5: Solve for Minimum Velocity v0
Rearranging the equation gives:
0.5v2=6×0.6
0.5v2=3.6
v2=3.60.5=7.2
v=√7.2=65√5m/s
Step 6: Work Done in Moving from Highest Point to Lowest Point
The work done on the sphere as it moves from the highest point to the lowest point can be calculated using:
W=Wg+We=ΔKE
Where:
- Work done by gravity, Wg=−mg⋅2r=−0.5⋅10⋅1.2=−6J
- Work done by the electric field, We=qE⋅2r=(110×10−6)⋅(105)⋅1.2=13.2J
Step 7: Set Up the Energy Equation
The change in kinetic energy from the highest point to the lowest point is given by:
Wg+We=12mv2−12mv20
Substituting the values:
−6+13.2=12⋅0.5⋅v2−12⋅0.5⋅(65√5)2
Step 8: Solve for Final Velocity v
After solving the above equation, we find:
7.2=12⋅0.5⋅v2−12⋅0.5⋅7.2
This leads to:
v2=36
Thus:
v=6m/s
Final Answer:
The minimum velocity of the sphere required at the highest point to just complete the circle is v=6m/s.
---
We have the following values provided in the problem:
- Mass of the sphere, m=0.5kg
- Charge of the sphere, q=110μC=110×10−6C
- Length of the string (radius of the circle), r=60cm=0.6m
- Electric field strength, E=105N/C
- Acceleration due to gravity, g=10m/s2
At the highest point of the circle, the forces acting on the sphere are:
1. Weight of the sphere, W=mg=0.5×10=5N (acting downward)
2. Electric force due to the electric field, Fe=qE=(110×10−6)×(105)=11N (acting upward)
At the highest point, for the sphere to just complete the circle, the centripetal force required is provided by the net force acting on it. The net force Fnet at the highest point can be expressed as:
Fnet=Fe−W
Substituting the values:
Fnet=11N−5N=6N
The net force acting on the sphere at the highest point provides the necessary centripetal force for circular motion:
mv2r=Fnet
Substituting the known values:
0.5v20.6=6
Rearranging the equation gives:
0.5v2=6×0.6
0.5v2=3.6
v2=3.60.5=7.2
v=√7.2=65√5m/s
The work done on the sphere as it moves from the highest point to the lowest point can be calculated using:
W=Wg+We=ΔKE
Where:
- Work done by gravity, Wg=−mg⋅2r=−0.5⋅10⋅1.2=−6J
- Work done by the electric field, We=qE⋅2r=(110×10−6)⋅(105)⋅1.2=13.2J
The change in kinetic energy from the highest point to the lowest point is given by:
Wg+We=12mv2−12mv20
Substituting the values:
−6+13.2=12⋅0.5⋅v2−12⋅0.5⋅(65√5)2
After solving the above equation, we find:
7.2=12⋅0.5⋅v2−12⋅0.5⋅7.2
This leads to:
v2=36
Thus:
v=6m/s
The minimum velocity of the sphere required at the highest point to just complete the circle is v=6m/s.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Exercise 3.3
Explore 9 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Subjective
Explore 28 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Exercise 3.1
Explore 23 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
A small sphere of mass m=0.6kg carrying a positive charge q=80μC is connected with a light, flexible, and inextensible string of length r=30cm and whirled in a vertical circle. If a horizontal rightward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
View SolutionTwo small particles A and B having masses m=0.5kg each and charges q1=(−155/18μC) and q2=(+100μC), respectively, are connected at the ends of a nonconducting, flexible, and inextensible string of length r=0.5m.
Particle A is fixed and B is whirled along a vertical circle with center at A. if a vertically upward electric field of Strength E=1.1×105NC−1 exists in the space, calculate the minimum velocity of particle B required at the highest point so that it may just complete the circle (g=10ms−2).
 .
.
View SolutionA stone of mass 2.0 kg is tied to the end of a string of 2m length. It is whirled in a horizontal circle. If the breaking tension of the string is 400 N, calculate the maximum velocity of the stone.
View SolutionThe maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
View SolutionOne end of a light rod of length 1m is attached with a string of length 1m. Other end of the rod is attached at point O such that rod can move in a vertical circle. Other end of the string is attached with a block of mass 2kg. The minimum velocity that must be given to the block in horizontal direction so that it can complete the vertical is (g=10m/s2)
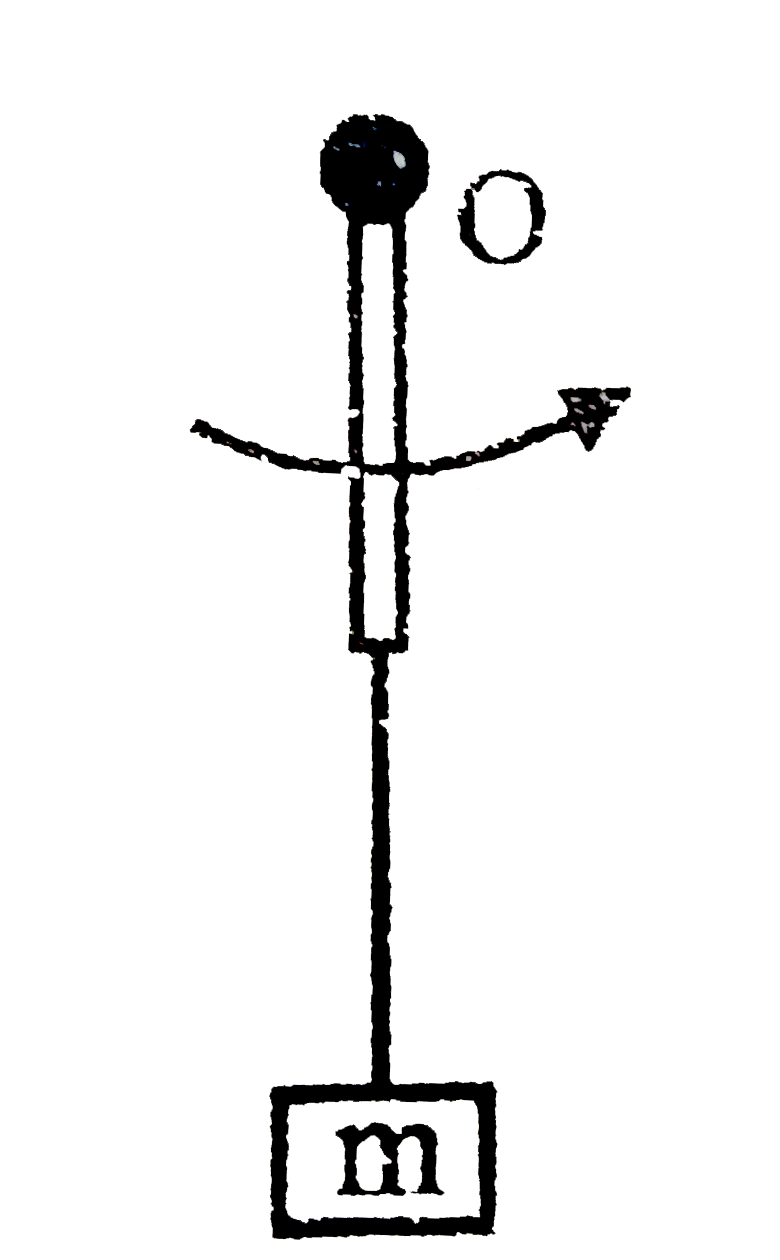
View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
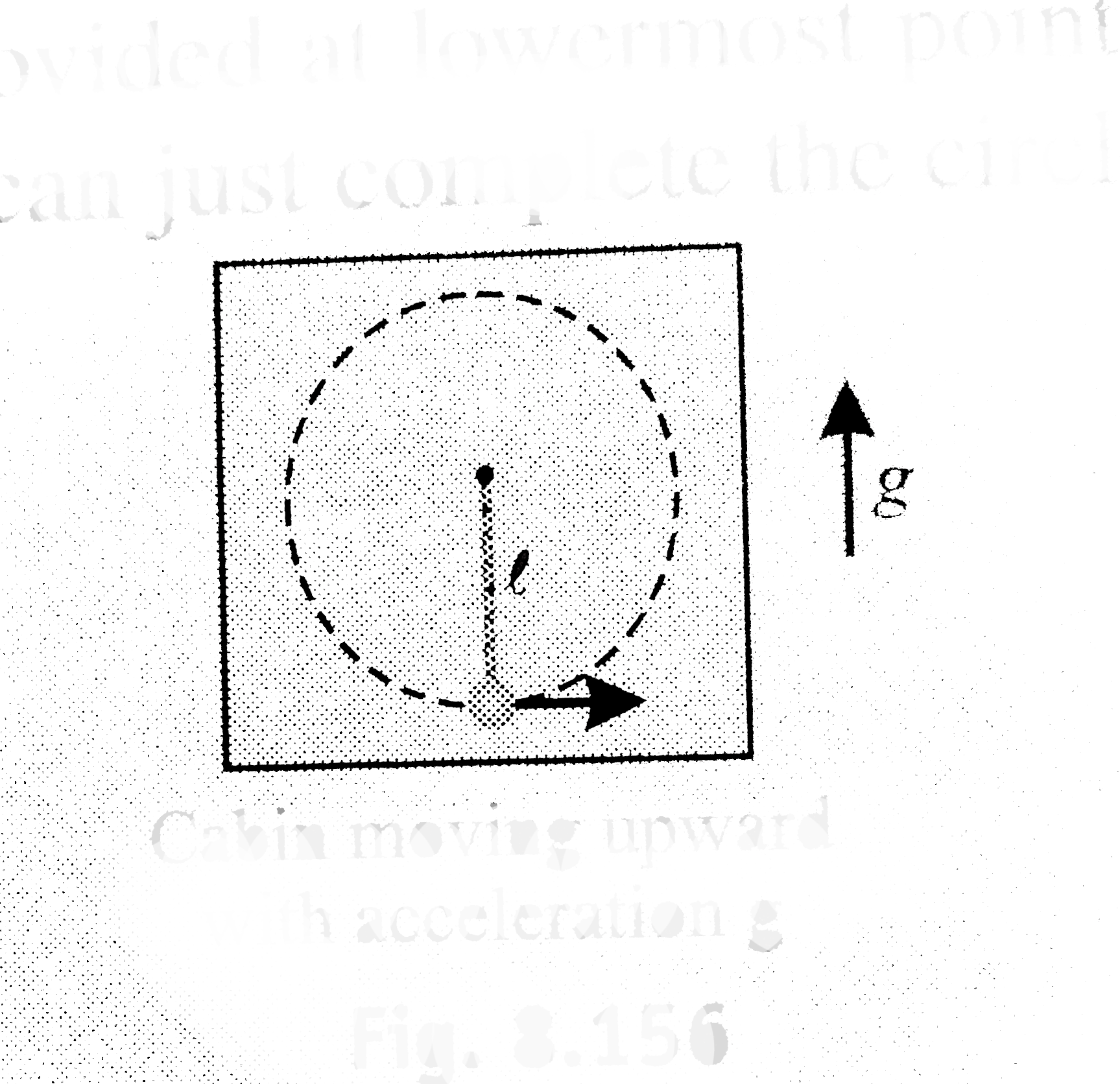
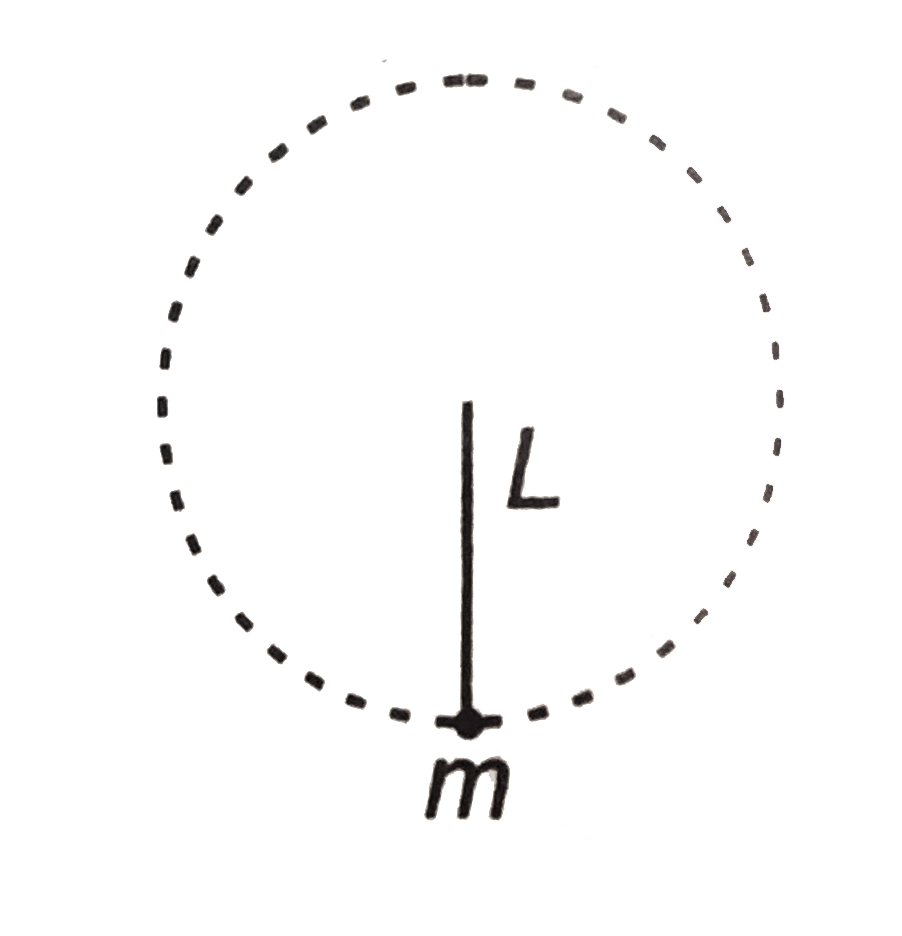
View SolutionA small particle of mass m attached with a light inextensible thread of length L is moving in a vertical circle. In the given case particle is moving in complete vertical circle and ratio of its maximum to minimum velocity is 2:1 .
Kinetic energy of the particle at the lower most position is
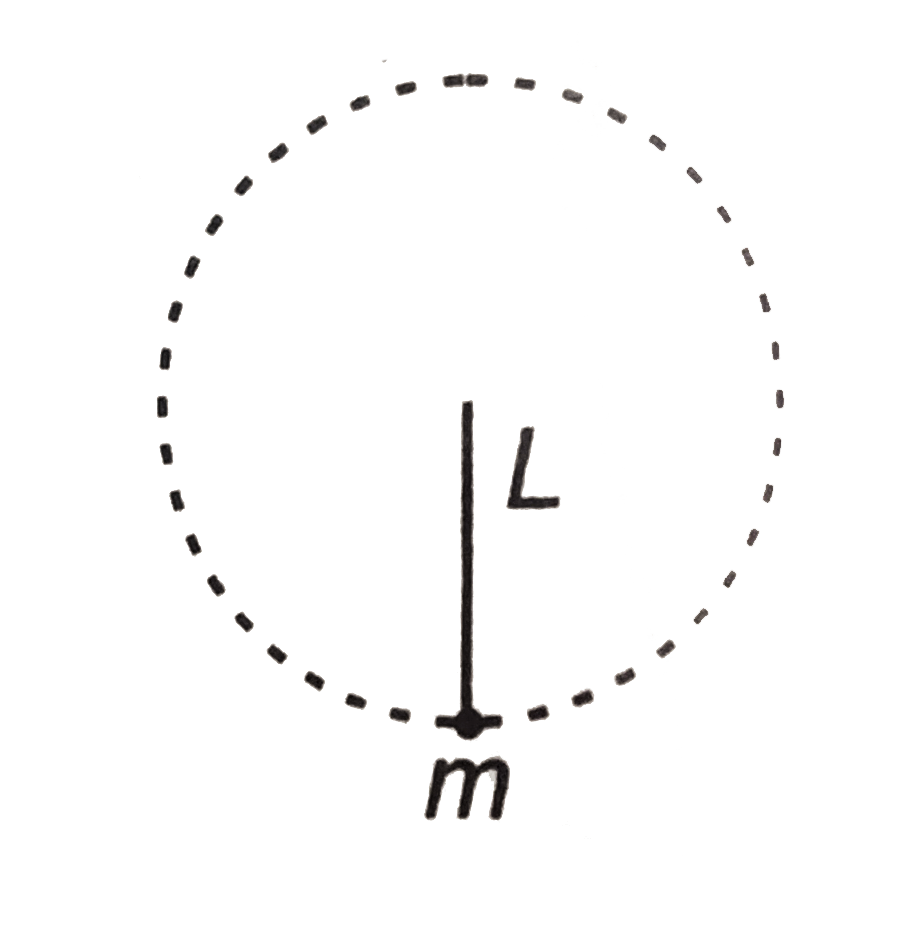
View SolutionA small particle of mass m attached with a light inextensible thread of length L is moving in a verical circle. In the given case particle is moving in complete vertical circle and ratio of its maximum to minimum velocity is 2:1 .
Minimum velocity of the particle is
View SolutionA particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
View Solution

