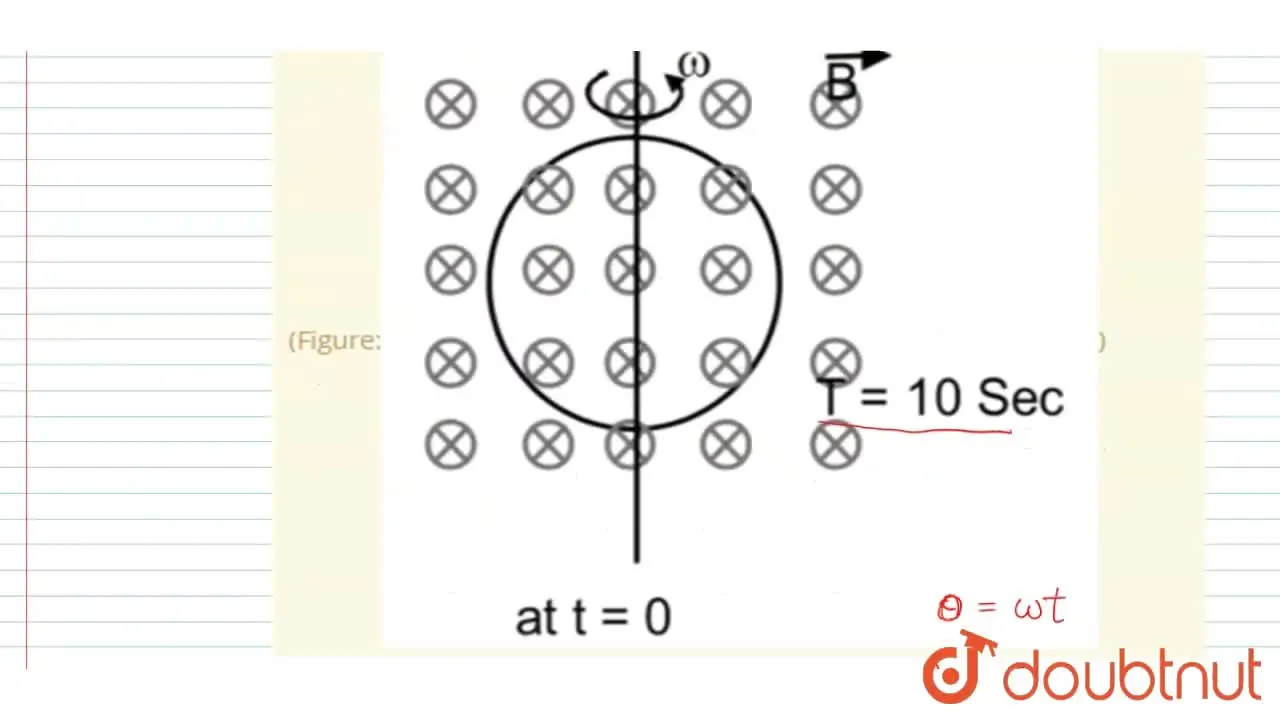
A ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure: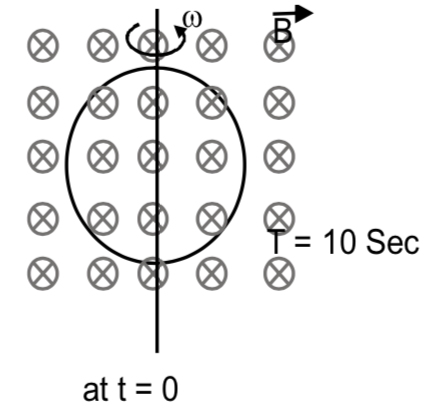
)
5 sec and 7.5 sec
2.5 sec and 5 sec
2.5 sec and 7.5 sec
10 sec and 5 sec
The correct Answer is:B
NA
Topper's Solved these Questions
Similar Questions
A ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field.If T=10sec, find the instant of time at which EMF will be maximum & minimum respectively :
View Solutionthe uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View Solution
Knowledge Check
- Question 1 - Select One
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
the uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
View SolutionA charge q is unifomly distrybuted over a nonconducting ring of radius R. The ring is rotated about an axis passing through its centre and perpendicular to the plane of the ring with frequency f. The ratio of electric potential to the magnetic field at the centre of the ring depends on.
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
View SolutionA circular conducting ring is rotated about one of its diameter in a magnetic field
View Solution