A point charge q is located at a distance l from an infinite conduting plane. Determine the surface density of charges induced on the plane as a function of separaction r from the base of the perpendicular drawn to the plane from the chagre.
The correct Answer is:σ=−ql2π(l2+r2)3/2,qnd=−q
Step by step video & image solution for A point charge q is located at a distance l from an infinite conduting plane. Determine the surface density of charges induced on the plane as a function of separaction r from the base of the perpendicular drawn to the plane from the chagre. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
View SolutionWhat is the perpendicular distance of the point
(6, 7, 5) from YZ-plane?View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
 View Solution
View SolutionFoot of perpendicular drawn from a point P(-2, 3, 5)
on the YZ-plane isView SolutionA point negative charge -Q is placed at a distance r from a dipole with dipole moment P in the xy plane as shown in fig. The x-component of force acting on the charge-Q is
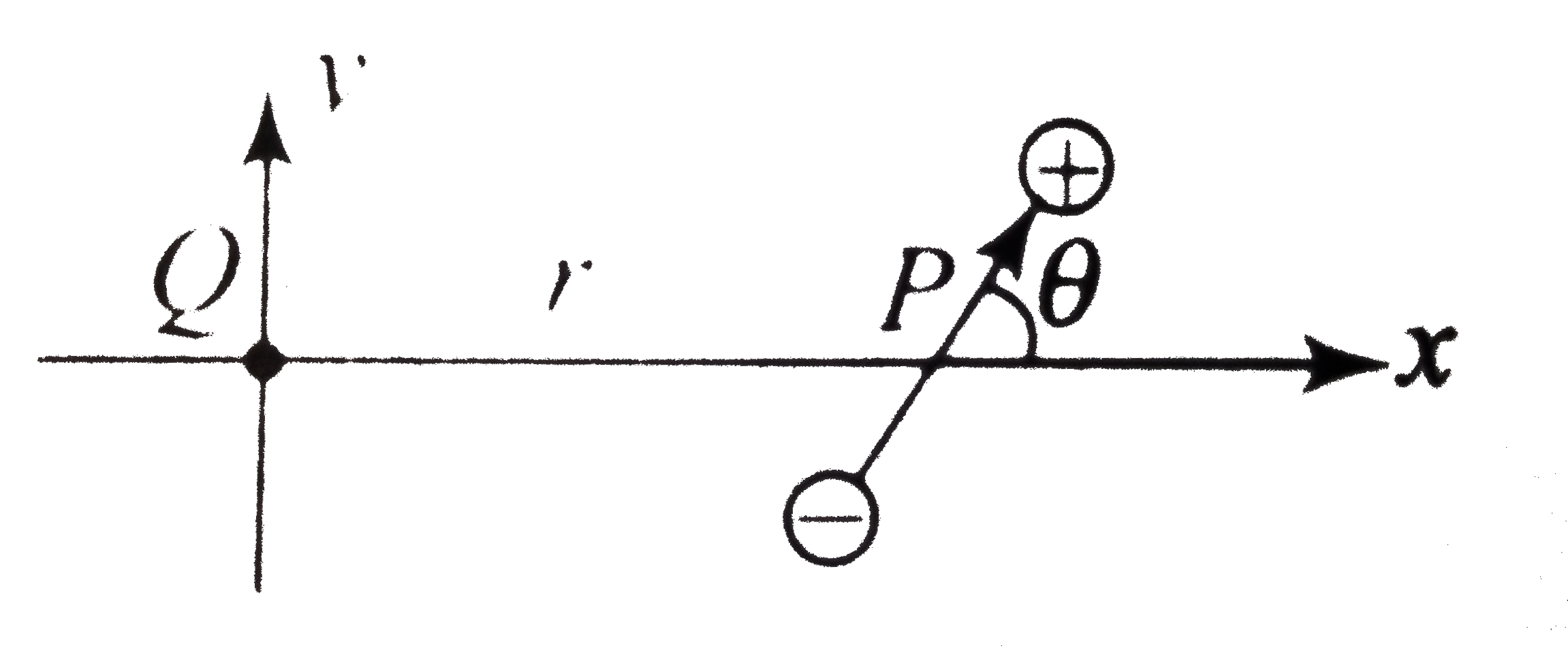 View Solution
View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View SolutionThe perpendicular distance of the point P(6, 8, 9)
from XY-plane isView SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png) View Solution
View Solution


