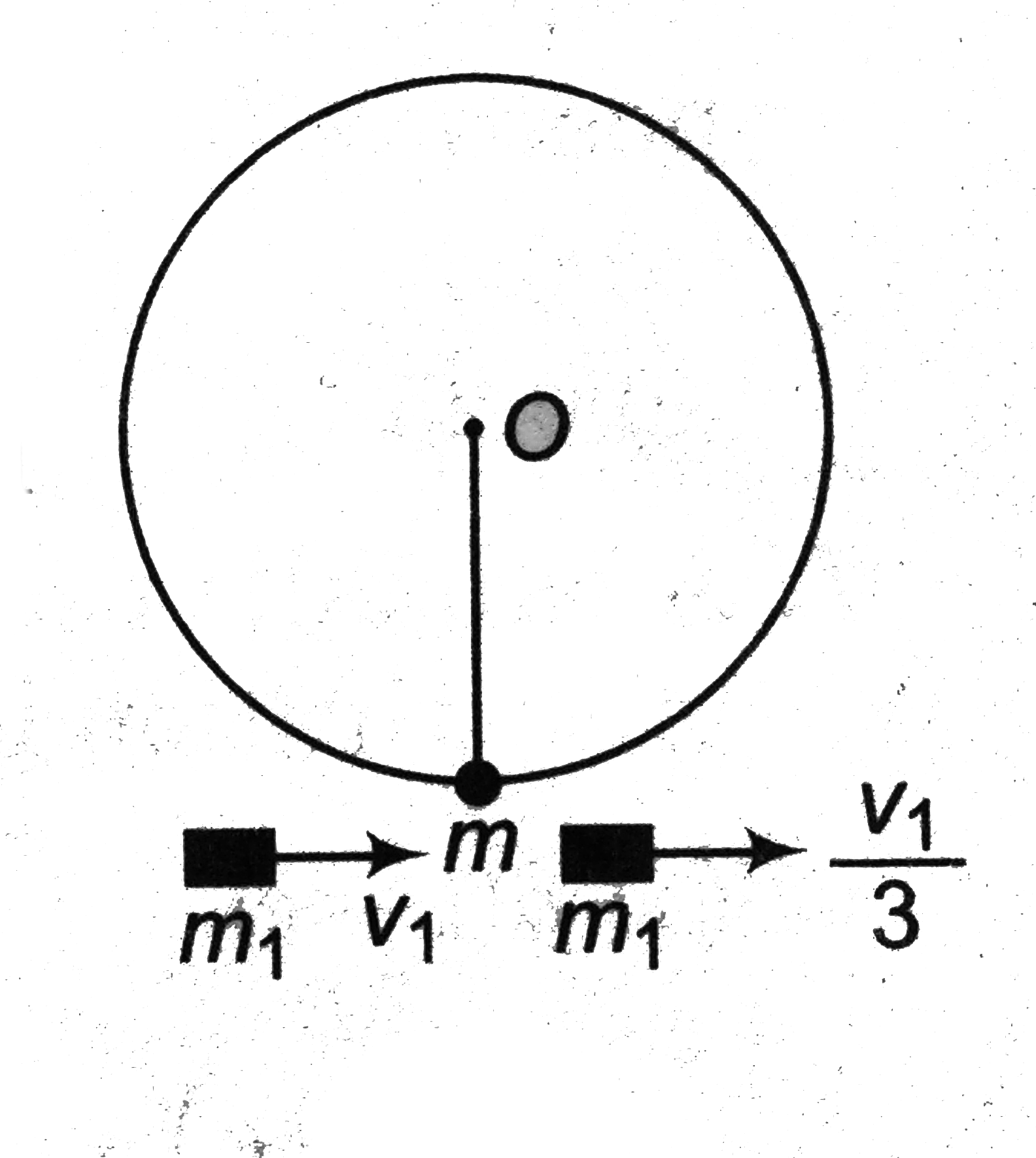
A pendulum comsists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1 and it emerges from the bob with speed v13. The bob just completes motion along a vertical circle. Then v1 is
(a) mm1√5gl
(b) 3m2m1√5gl
(c) 23(mm1)√5gl
(d) (m1m)√gl
The correct Answer is:B
Let velocity of m just after collision is v. Then, from conservation of momentum we have,
m1v1=mv+m1v13⇒∴v=23m1v1m
Now, for just completing the circle,
v=√5gl
∴23m1v1m=√5gl
∴v1=3m2m1√5gl
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Single Correct Option
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob is just able to complete the circular motion, then tension at the lowest point just when the bob starts rising will be
View SolutionA pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob stops where the string becomes horizontal then v is
View Solution
Knowledge Check
A pendulum consists of a wooden bob of mass m and of length L. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed v1/3 and the just completes motion along a vertical circle. Then v1 is:
A(mm1)√5glB32(mm1)√5glC23(mm1)√5glD(m1m)√glA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
A3m2m1√5glBm1m√5glC2m3m1√5glDm1m√glA pendulum consists of a wooden bob of mass in and of length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed (v1)/3 and the bob just completes motion along a vertical circle. Then v1is
A(mm1)√5glB32(mm1)√5glC23(m1m)√5glD(m1m)√gl
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
What is the momentum transferred to the bob by the bullet?
View SolutionA simple pendulum of bob of mass m and length L has one of its ends fixed at the centre O of a vertical circle, as shown in the figure. If 0=60∘ at the point P, the minimum speed u that should be given to the bob so that it completes vetical circle is
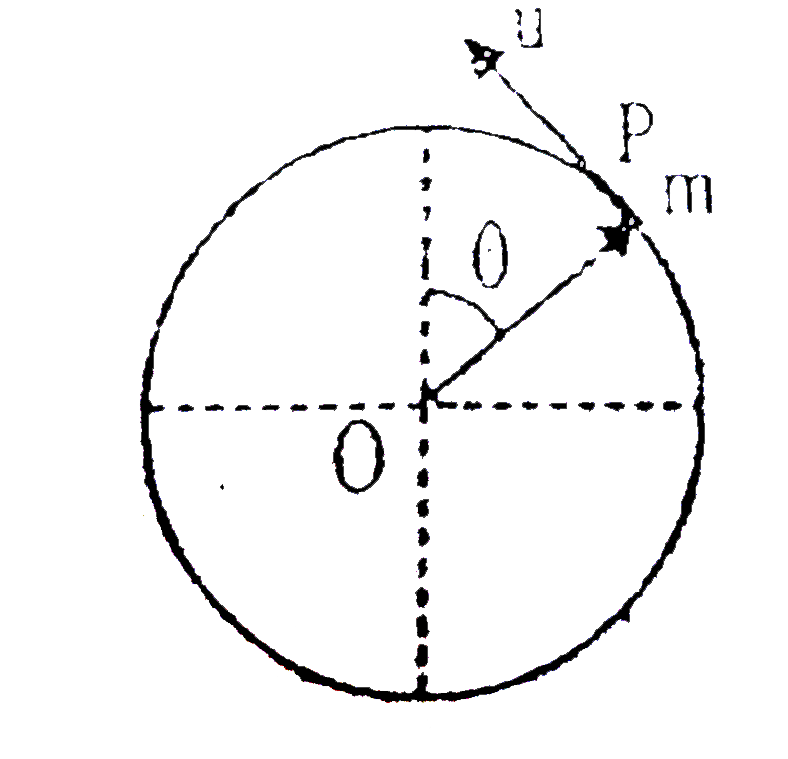
View SolutionA simple pendulum bob of mass M and length l has one of its end fixed at the centre of a vertical circle as shown in figure. If θ=60∘ at the point P, the minimum speed u that should be given to the bob so that it completes vertical circle is :

View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View SolutionA bullet of mass m passes through a pendulum bob of mass M with velocity v and comes out of it with a velocity v2. The minimum value of v so that the bob completes one revolution in the vertical circle is (l = length of pendulum)
View Solution

