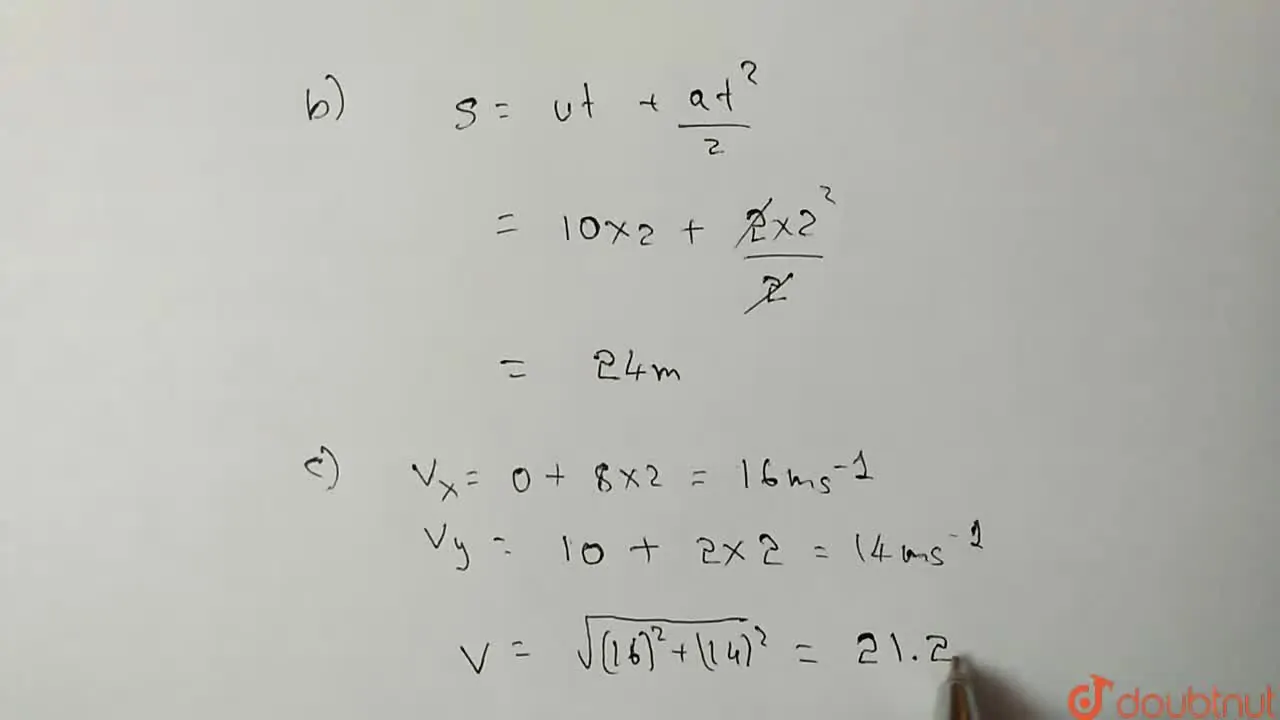A particle starts from origin t = 0 with velocity 10.0ˆjms−1 and moves in the x−y plane with a constant acceleration of 8.0ˆi+2.0ˆjms−2
(a) At what time the x - coordinate of the particle is 16 m?
(b) What is the y - coordinate of the particle at the time?
(c) What is the speed of the particle at that time?Solution in Kannada
Given →vy=10.0ˆjandvy=10ms−1
→a=(8.0ˆt+2.0ˆj)ms−2
i.e., |→ax|=8.0ms−2and∣∣→ay∣∣=2.0ms−2
but →v=→v0+→at
i.e., →v=10ˆj+(8.0ˆi+2.0ˆj)t
∴ →v=8.0ˆit+(10+2.0t)ˆj
→s=→vyt+12→at2=10ˆjt+12(8ˆi+2ˆj)t2=10ˆjt+(4ˆi+ˆj)t2
=(4t2)ˆi+(10t+t2)ˆj
→s=sxˆt+syˆj
Where sx=4t2andsy=10t+t2
t2=sx4=164 sy=10(2)+22
t=2s =24m
vx=8×2=16ms−1andvy=2×2+10=14ms−1
Where v=√v2x+v2y=√162+142=21.26ms−1
Related Playlists
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - FIVE MARKS QUESTIONS WITH ANSWERS3videos
MOTION IN A STRAIGHT LINE
- BOOK - SUBHASH PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NUMERICALS WITH SOLUTIONS11videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN PLANEEXERCISE - NUMERICALS WITH SOLUTIONS47videos
MOTION IN PLANE
Similar Questions
Show that v=v0+at by graphical method.
03:02View SolutionCalculate the percentage increase in length of a wire of diameter 0.40 mm, stretched by a load of 5 kg. (Given: Young's modulus of elasticity of material of the wire 12.5×1010Nm−2)
01:28View SolutionTwo forces 8N and 5N are acting at a point on a body at an angle 120∘ then find the (i) magnitude and (ii) direction of their resultant.
04:02View SolutionA particle starts from the origin at t=0 with a velocity of 10.0 hat j m//s and moves in the X-y plane with a constant accleration of ( 8.0 hat I + 2. 0 hat j ) ms^(-2) . (a) At wht time is the s-coordinate of the particle 16 m ? What is the y-coordinate of the particle at that time ? ( b) What is the speed of the particle at that time ?
03:41View SolutionA particle starts from the origin at t=Os with a velocity of 10.0ˆjm/s and moves in the xy-plane with a constant acceleration of (8ˆi+2ˆj)m/s−2. What time is the x-coordinate of the particle 16m?
View SolutionA particle starts from origin at t = 0 with a velocity 5.0hati m//s and moves in x-y plane under action of a force which produces a constant acceleration of (3.0hati+2.0hati)m//s^(2) : (a) What is the y-coordinate of the particle at the instant if its x-coordinate is 84m? (b) What is the speed of the particle this time?
05:37View SolutionA particle stars from origin at t=0 with a velocity 5.0hatim//s and moves in x-y plane under action of a force which produces a constant acceleration of (3.0hati+2.0hatj) m//s^(2) . (a) What is the y- coordinate of the particle at the instant its x - coordinate is 84 m ? (b) What is the speed of the particle at this time ?
View SolutionA particle starts from the origin at t=0 s with a velocity of 10.0hatjm//s and moves in the x-y plane with a constant acceleration of (8.0hati+2.0hatj) " m s"^(-2) (a) At what time is the x - coordinate of the speed of the particle at the time ?
View SolutionA particle stars from origin at t=0 with a velocity 5.0ˆim/s and moves in x-y plane under action of a force which produces a constant acceleration of (3.0ˆi+2.0ˆj)m/s2. (a) What is the y- coordinate of the particle at the instant its x - coordinate is 84 m ? (b) What is the speed of the particle at this time ?
06:04View SolutionA particle stars from origin at t=0 with a velocity 5.0hatim//s and moves in x-y plane under action of a force which produces a constant acceleration of (3.0hati+2.0hatj) m//s^(2) . (a) What is the y- coordinate of the particle at the instant its x - coordinate is 84 m ? (b) What is the speed of the particle at this time ?
06:35View SolutionA particle starts from the origin at t=0 s with a velocity of 10.0ˆjm/s and moves in the x-y plane with a constant acceleration of (8.0ˆi+2.0ˆj) m s−2 (a) At what time is the x - coordinate of the speed of the particle at the time ?
06:31View SolutionA particle stars from origin at t=0 with a velocity 5.0hatim//s and moves in x-y plane under action of a force which produces a constant acceleration of (3.0hati+2.0hatj) m//s^(2) . (a) What is the y- coordinate of the particle at the instant its x - coordinate is 84 m ? (b) What is the speed of the particle at this time ?
View SolutionA particle starts from the origin at t=0 s with a velocity of 10.0ˆjm/s and moves in the x-y plane with a constant acceleration of (8.0ˆi+2.0ˆj) m s−2 (a) At what time is the x - coordinate of the speed of the particle at the time ?
View SolutionA particle starts from the origin at t=0 with a velocity of 10.0 hat j m//s and moves in the x-y plane with a constant acceleration of ( 8.0 hat i + 2. 0 hat j ) ms^(-2) . (a) At what time is the x-coordinate of the particle 16 m ? What is the y-coordinate of the particle at that time ? (b) What is the speed of the particle at that time ?
View SolutionA paricle starts from the origin at t = 0s with a velocity of 10.0ˆjm/s and moves in the xy-plane with a constant acceleration of (8.0ˆi+2.0ˆj)ms−2. What time is the x-coordinate of the particle 16m?
04:52View Solution