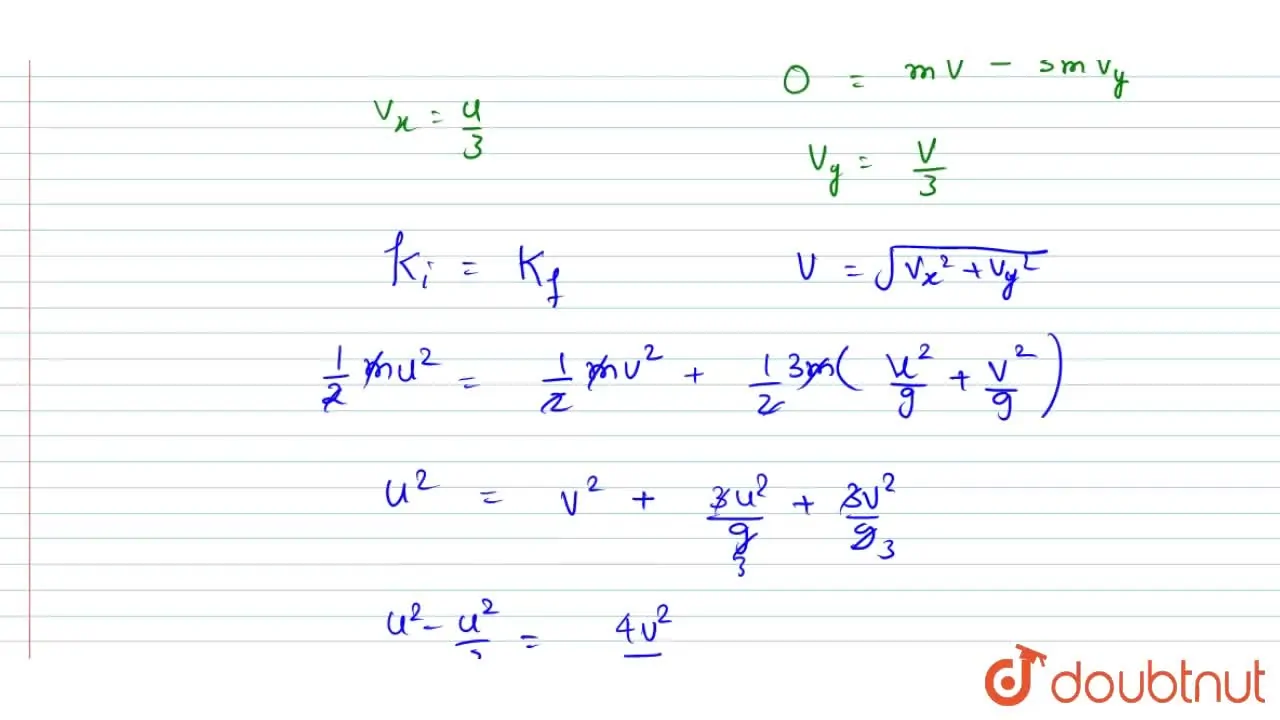A particle of mass m with an initial velocity uˆi collides perfectly elastically with a mass 3 m at rest . It moves with a velocity vˆj after collision , then , v is given by :
v=√23u
v=1√6u
v=u√3
v=u√2
Step by step video & image solution for A particle of mass m with an initial velocity u hati collides perfectly elastically with a mass 3 m at rest . It moves with a velocity vhatj after collision , then , v is given by : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m with an initial velocity uˆi+2uˆj collides with a particle of mass 3m at rest. After collision, the two particles stick together and the combined particle moves with a velocity vˆi+v'ˆj. Which of the following is incorrect?
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionTwo particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
View SolutionA body of mass m moving with velocity uˆi collides elastically with a body at rest of mass 3m and then the final velocity of body mass m is v ˆj. Find the relation between v and u
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.
 View Solution
View SolutionA particle moving with velocity (2ˆi−3ˆj) m/s collides with a surface at rest in xz–plane as shown in figure and moves with velocity (2ˆi+2ˆj) m/s after collision. Then coefficient of restitution is :
 View Solution
View Solution