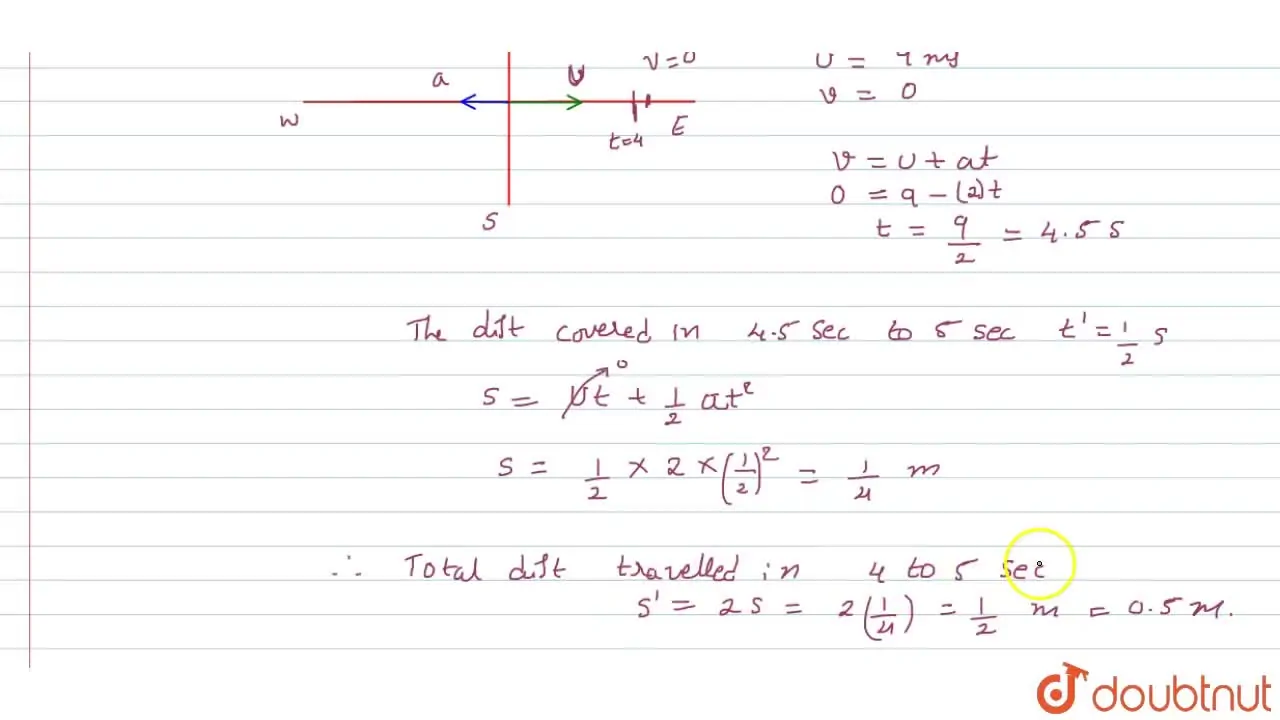
A particle moving with constant acceleration of 2m/s2 due west has an initial velocity of 9 m/s due east. Find the distace covered in the fifth second of its motion. Solution in Kannada
Initial velocity u = +9 m/s
Acceleration a = - 2 m/s2
In this problem, acceleration.s direction is opposite to the velocity.s direction.
Let .t. be the time taken by the particle to reach a point where it makes a turn along the straight line. we have , v = u + at
O = 9 - 2 t
We get , t = 4.5s
Now let us find the distace convered in 12 second i.e. from 4.5 to 5 second Let u at t = 4.5 sec.
Then distance convered in 12 s.
s=12at2
s =12×2×[12]2
=14 m
Total distance covered in fifth second of its motion is given by
S0=2s=2(14)=12m .

Related Playlists
- BOOK - NCERT KANNADCHAPTER - MOTIONEXERCISE - LET US IMPROVE OUR LEARNING (REFLECTIONS ON CONCEPTS )1videos
MOTION
- BOOK - NCERT KANNADCHAPTER - MOTIONEXERCISE - LET US IMPROVE OUR LEARNING(APPLICATION OF CONCEPTS)6videos
MOTION
- BOOK - NCERT KANNADCHAPTER - MATTER AROUND USEXERCISE - Let us Improve our learning (Suggested project)1videos
MATTER AROUND US
- BOOK - NCERT KANNADCHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - II. Application of concepts1videos
REFRACTION OF LIGHT AT PLANE SURFACES
Similar Questions
Distinguish between speed and velocity
01:56View SolutionA train of length 50m is moving with a constant speed of 10m/s. Calculate the time taken by the train to cross an electric pole and a bridge of length 250 m. (5s , 30s) (AS1)
04:39View SolutionWhat are the factors affecting the rate of diffusion?
02:05View SolutionA light ray is incident on air-liquid interface at 45∘ and is refracted at 30∘. What is the refractive index of the liquud? For what angle of incidence will the angle between reflected ray and refracted ray be 90∘?(AS7)
04:48View SolutionAnoop is moving due east with a velocity of 1m/s and Dhyani is moving due west with a velocity of 2m/s. what is the velocity of Anoop with respect to Dhyani?
03:27View SolutionA particle has an initial velocity of 5.5ms−1 due east and a constant acceleration of 1ms−2 due west. The distance covered by the particle in sixth second of its motion is.
01:51View SolutionSeeta is moving due east with a velocity of V1m/s and geets iss moving due west with velocity of V2m/s. The velocity of Seeta with respect to Geeta is
06:42View SolutionA particle has an initial velocity of 9m/s due east and a constant acceleration of 2m/s2 due west. The displacement coverd by the particle in the fifth second of its motion is :
03:02View SolutionA particle has initial velocity of 17 ms^(-1) towards east and constant acceleration of 2 ms^(-2) due west. The distance covered by it in 9th second of motion is :
05:01View SolutionA particle has initial A particle has initial velocity 10m//s . It moves due to constant retarding force along the line of velocity which produces a retardation of 5 m//s^(2) . Then
09:14View SolutionA particle moving with constant acceleration of 2m/s2 due west has an initial velocity of 9m/s due east. Find the distance covered in the fifth second of its motion.
06:42View SolutionA particle moves in a straight line with constant acceleration If it covers 10 m in first second and 20 m in next second find its initial velocity.
05:30View SolutionA particle moving with constant acceleration of 2m/ s^(2) due west has an initial velocity of 9 m/s due east. Find the distace covered in the fifth second of its motion.
03:44View SolutionA particle moving with constant acceleration of 2m/ s^(2) due west has an initial velocity of 9 m/s due east. Find the distace covered in the fifth second of its motion.
01:36View SolutionA particle moving with constant acceleration of 2m/ s^(2) due west has an initial velocity of 9 m/s due east. Find the distace covered in the fifth second of its motion.
04:51View Solution