A liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

The correct Answer is:A, B, C
From, A1v1=A2v2 or v∝14
At a point where area of cross-section is less, volume of liquid flowing per second is same but speed is more. Therefore, here kinetic energy is more or the pressure will be less.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Medical entranes gallery
Explore 49 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:B) Medical entrance special format question
Explore 19 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Current is flowing through a wire of non-uniform cross section. Cross section of wire at A is les than the cross section of wire at B. Then match the following
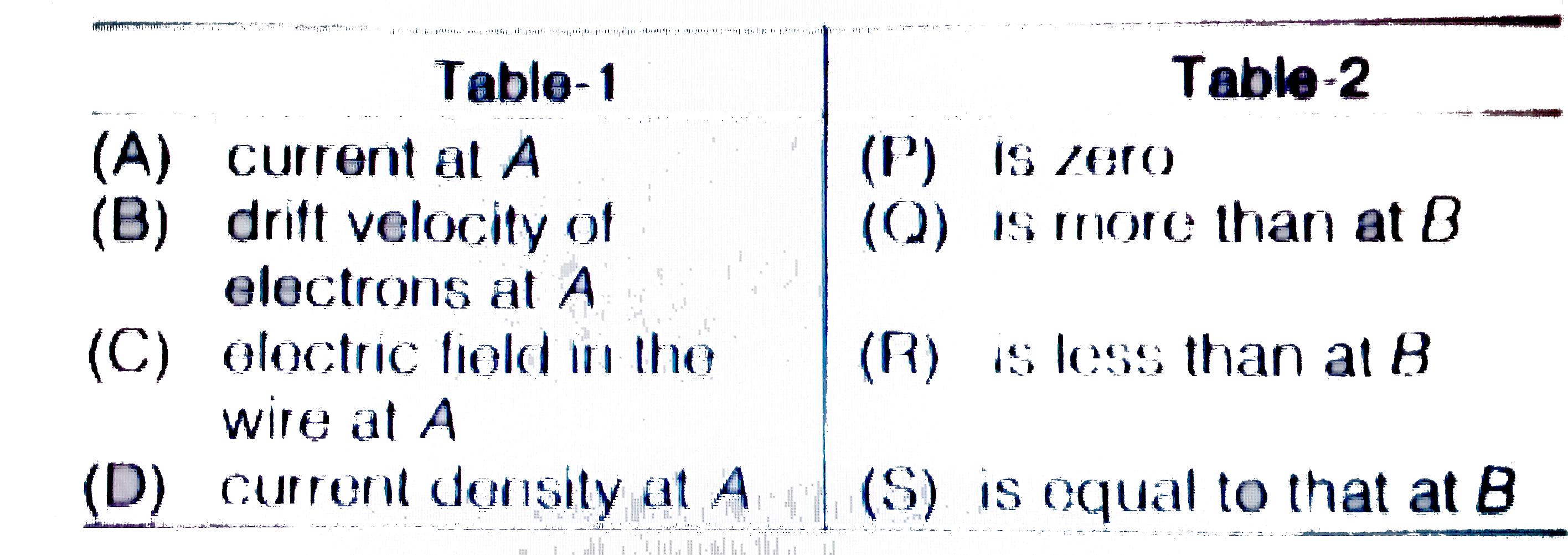
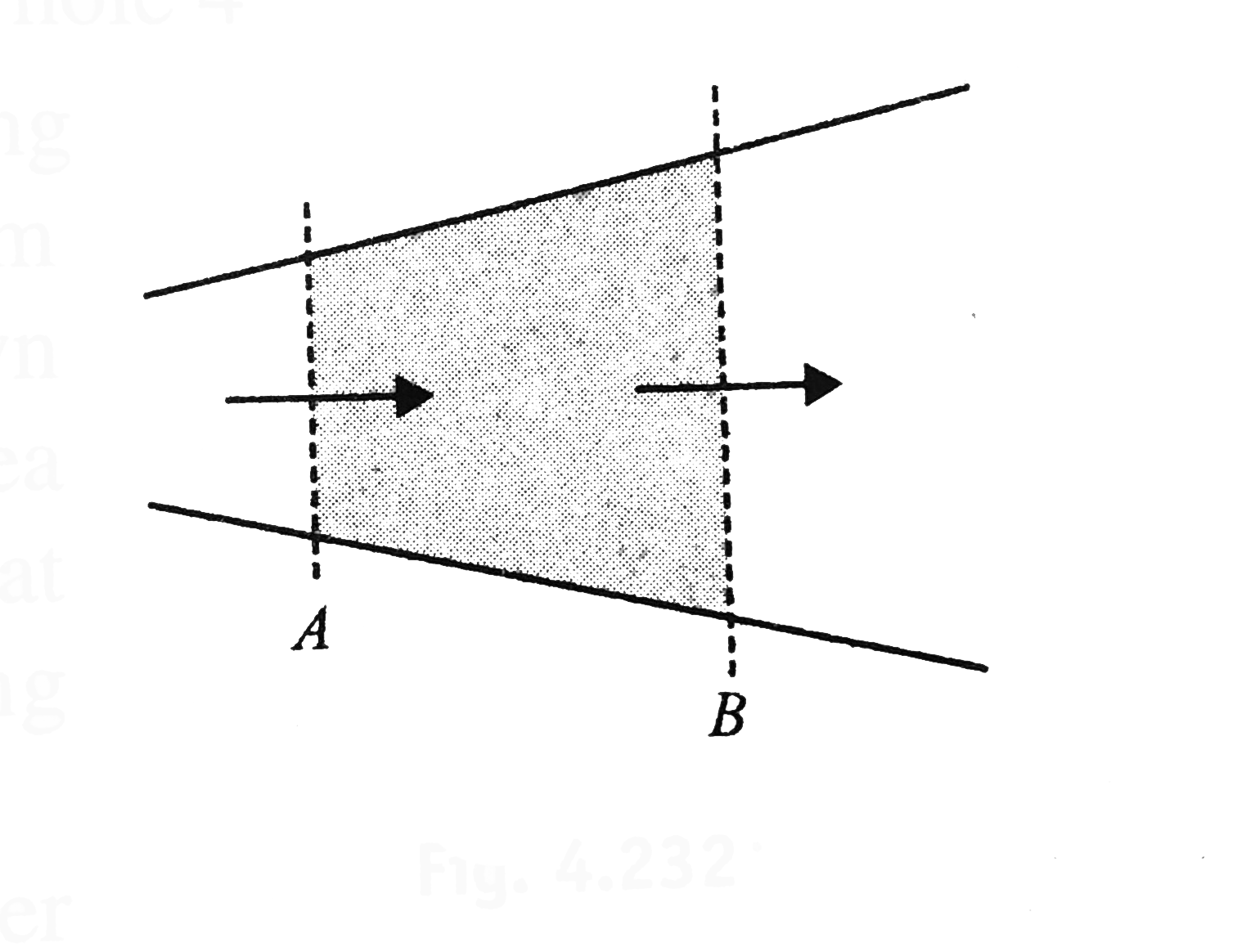
View SolutionA non-viscous liquid is flowing through a non-uniform pipe from section A to section B as shown in the figure. Cross sectional area of the pipe at A is less than that at B. Which of the following statements are correct?
View SolutionAssertion : When an ideal fluid flows through a pipe of non-uniform cross-section, then pressure is more at that section where area is more if the pipe is horizontal.
Reason : According to Bernoulli's theorem speed at broader cross-section will be less.
View SolutionA stready current i is flowing through a conductor of uniform cross-section. Any segment of the conductor has
View SolutionWater is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View Solutionwater is flowing through a tube of non-uniform cross-section. If the radii of the tube at the entrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
View SolutionWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
View SolutionConsidering a wire of non-uniform cross-section as shown.If the area of cross-section at A is double of the area of cross-section at point B.Ratio of heat energy dissipated in a unit volume per unit time at points A and B is
_PHY_E05_279_Q01.png)
View SolutionA liquid is flowing in a horizontal pipe of non-uniform cross section. Which of the following quantities may remain unchanged with respect to time?
View SolutionAssertion : If a current is flowing through a conducting wire of non-uniform cross-section, drift speed and resistance both will increase at a section where cross-sectional area is less.
Reason : Current density at such sections is more where cross-sectional area is less.
View Solution

