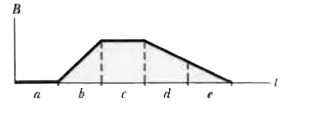
A graph between the magnitude of the magnetic flux linked with a closed loop and time is given in the figure. Arrange the regions of the graph in ascending order of the magnitude of induced emf in the loop.
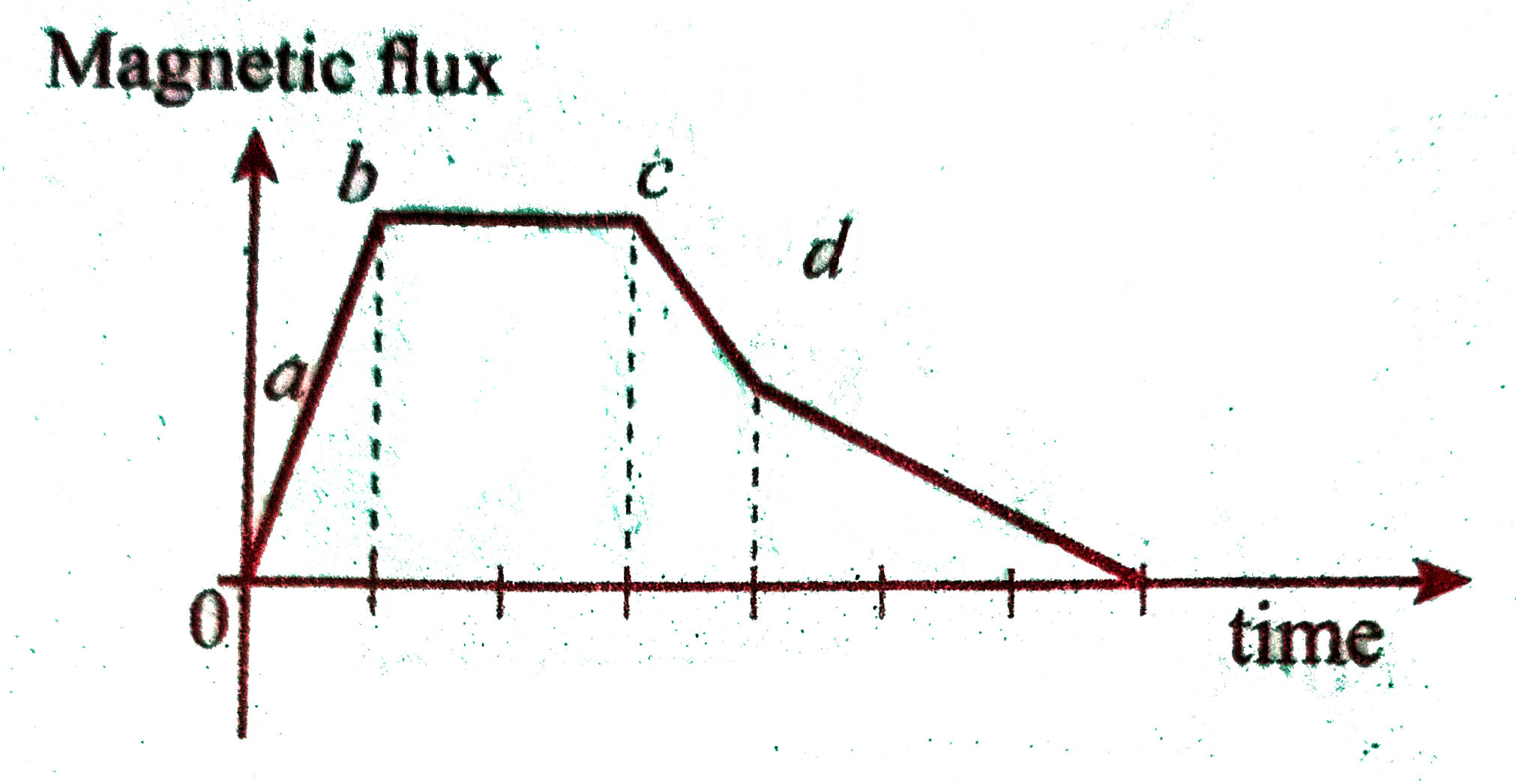
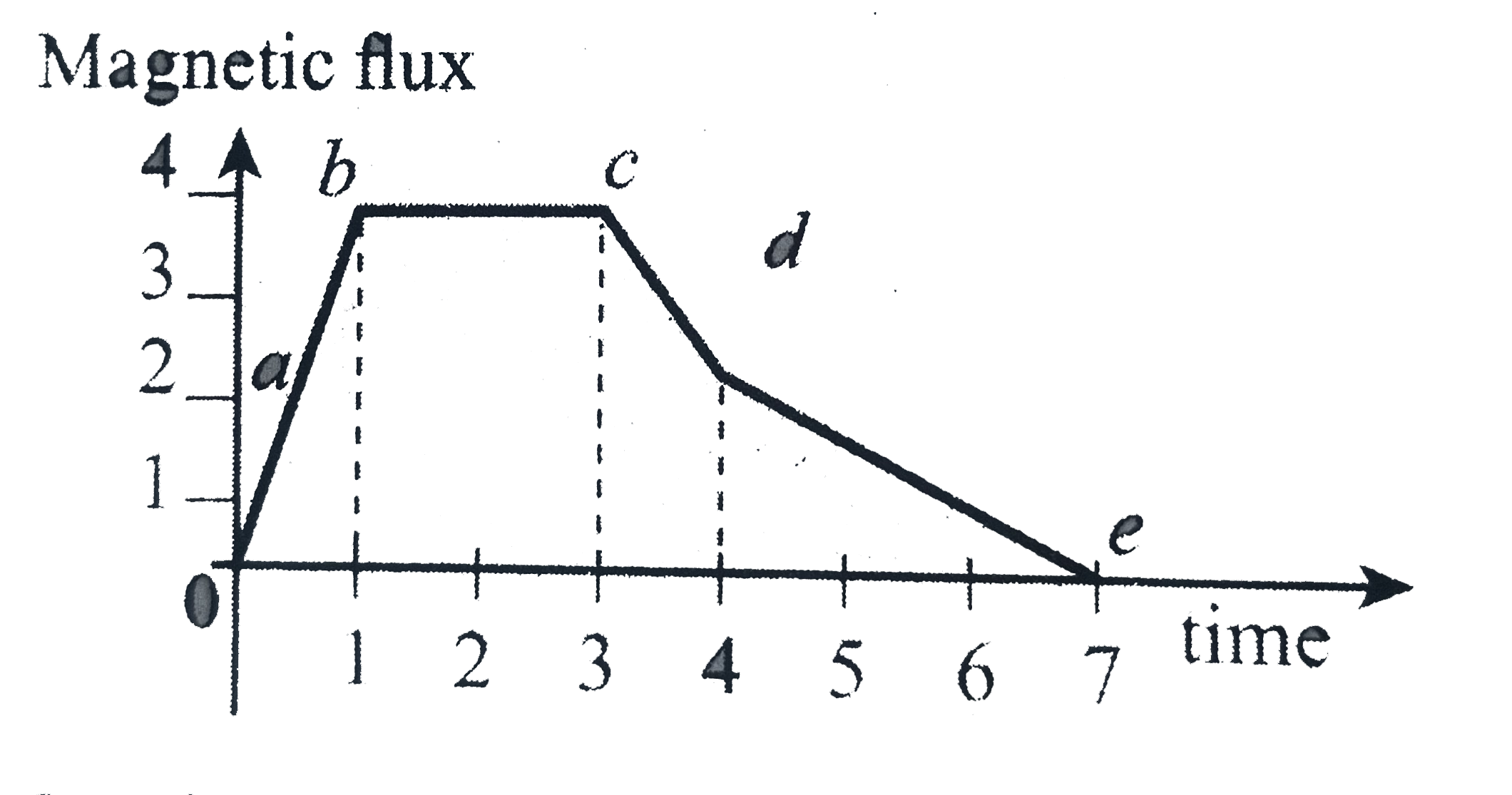
Magnitude of induced emf
|e|=∣∣∣−dϕdt∣∣∣=dϕdt
(i) In the region ab
e1=eϕ1dt=4−01−0=41=4V
(ii) In the region bc
e2=∣∣∣dϕ2dt∣∣∣=4−43−1
=02=0V
(iii) In the region cd
e3=∣∣∣dϕ3dt∣∣∣=2−07−4=23=0.66V
∴e2<e4<e3<e1
In the ascending order, magnitude of induced emf is region bc<region de<region cd<region ab
Similar Questions
Figure shows a graph between the magnitude of magnetic field passing normally through a closed loop and time t. Rank the five region's of the graph according to the emf in magnitude indụced in the loop, greatest first.
View SolutionThe magnitude off magnetic moment of the current loop in the figure is

View Solution
Knowledge Check
The magnitude of magnetic moment of the current loop in the figure is
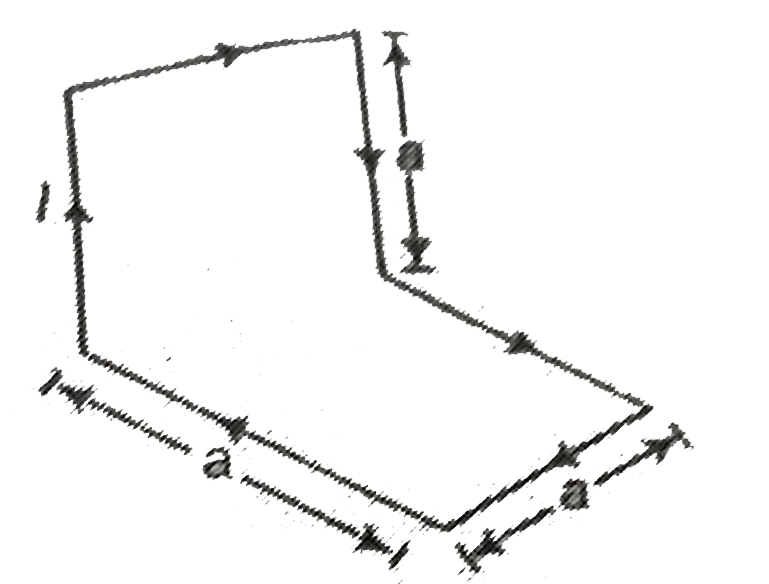 Ala2B√2la2CzeroDnone of the above
Ala2B√2la2CzeroDnone of the aboveThe graph gives the magnitude B (t) of a uniform magnetic field that exists throughout a conducting loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first
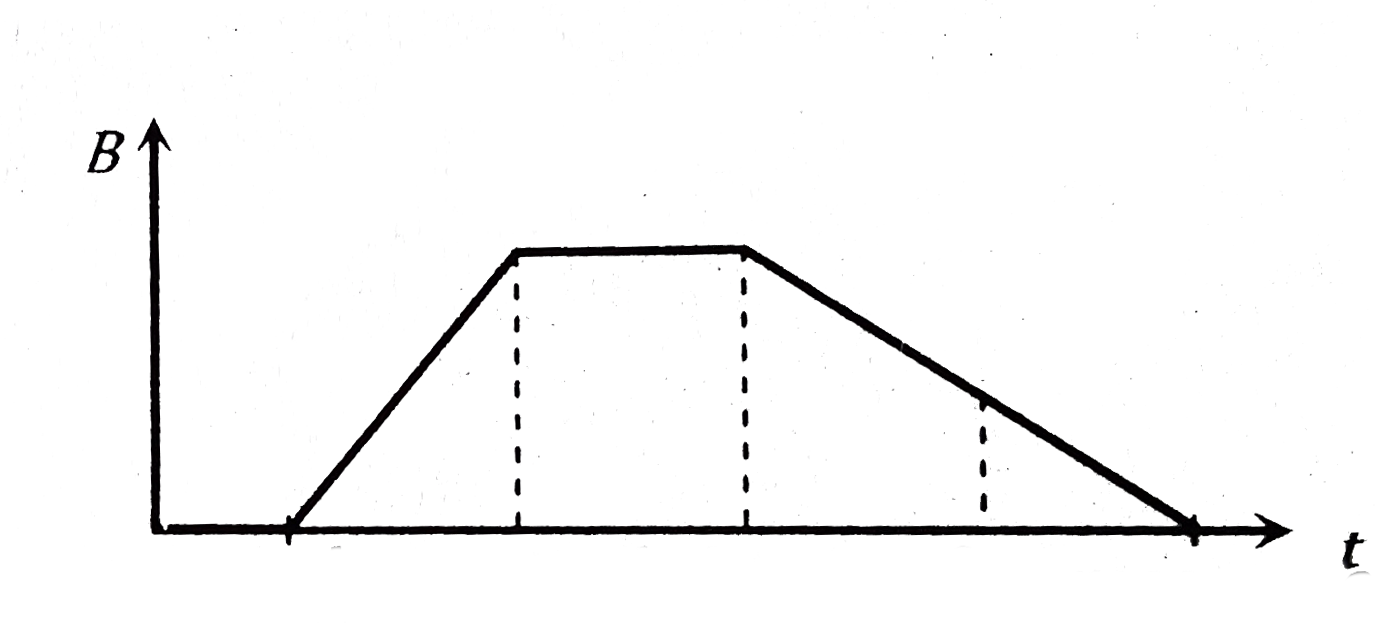 Ab>(d=e)<(a=c)Bb<(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
Ab>(d=e)<(a=c)Bb<(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first
 Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first

View SolutionThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.
View SolutionThe rate of change of magnetic flux linked with the coil is equal to the magnitude of induced e.m.f.' this is the statement of
View SolutionThe magnetic flux linked with a coil (in Wb) is given by the equation ϕ=5t2+3t+16 . The magnetic of induced emf in the coil at fourth second will be
View SolutionThe magnetic flux linked with a coil, in webers is given by the equation ϕ=3t2+4t+9. Then, the magnitude of induced emf at t = 2 s
View Solution

