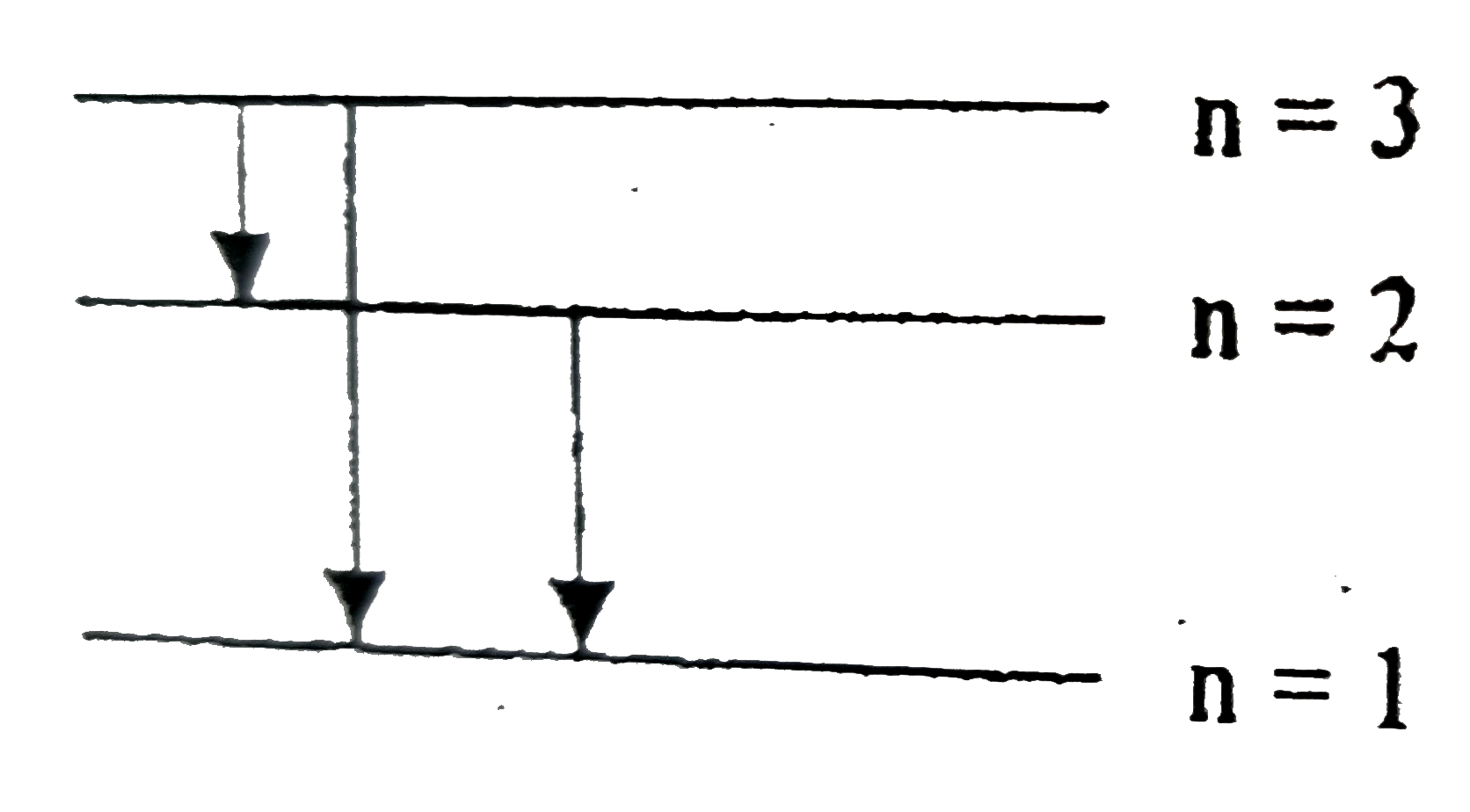
A gas hydrogen like atoms can absorb radiations of 68eV. Consequently, the atoms emit radiations of only three different wavelengths. All the wavelengths are equal or smaller than that of the absorbed photon.
(a) Determine the initial state of the gas atoms.
(b) Identify the gas atoms.
(c) Find the minimum wavelength of the emitted radiation.
(d) Find the ionization energy and the respective wavelength for the gas atoms.
(a) Since three radiations are emitted, therefore, the final excited state of the gas is n=3.
The initial state of the gas atoms is
n=2 as all the wavelengths are smaller and the energy will be higher.
(b) 13.6Z2[122−132]=68
or 13.6Z2[536]=68⇒Z=6
(c) The minimum wavelength corresponds to the transition n=3 to n=1.
1λmin=RZ2[112−132]
or λmin=98RZ2=98(1.097×107)(6)2=28.5Å
(d) The ionization energy of the gas atoms is
E=13.6Z2=(13.6)(6)2=489.6eV
λ=1RZ2=1(1.097×107)(6)2=25.32Å
Related Playlists
- BOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Illustration10videos
MODERN PHYSICS
- BOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Solved Problems10videos
MODERN PHYSICS
- BOOK - FIITJEECHAPTER - MAGNETISM AND MATTEREXERCISE - ASSIGNMENT PROBLEMS OBJECTIVE : (LEVEL -II) (MULTI CHOICE SINGLE CORRECT)20videos
MAGNETISM AND MATTER
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - NUMERICAL BASED QUESTIONS2videos
OPTICS
Similar Questions
Hydrogen atom absorbs radiations of wavelength λ0 and consequently emit radiations of 6 different wavelengths, of which two wavelengths are longer than λ0. Chosses the correct alternative(s).
View SolutionFind the minimum wavelength emitted by a hydrogen atom due to electronic transition.
View SolutionFind the wavelength of the emitted radiation,if electron in hydrogen atom jumps from third orbit to second orbit.
View SolutionWhich one among the following transitions of electron of hydrogen atom emits radiation of the shortest wavelength ?
View SolutionThe maximum wavelength of radiation that can ionize a sodium atom is 2414 A the ionization energy of sodium per mole shall be
View SolutionThe ionization potential of hydrogen atom is 13.6 eV. The wavelength of the energy radiation required for the ionization of H-atom
View SolutionWhich of the following transitions of an electron in hydrogen atom emits radiation of the lowest wavelength?
View SolutionA hydrogne like atom is excited using a radiation . Consequently, six spectral line are observed in the spectrum. The wavelegth of emission radiation is found to be equal or smaller than the radiation used for excitation. This concludes that the gas was initially at
View SolutionIf the electron in the hydrogen atom jumps from third orbit to second orbit the wavelength of the emitted radiation in term of Rydberg constant is
View SolutionThe maximum wavelength that a sample of hydrogen atoms can absorb is
View Solution


