A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?
(a) 2h3
(b) 5h4
(c) 5h3
(d) 5h2
The correct Answer is:C
Consider the equilibrium of wooden block. Forces acting in the downward direction are
(a) Weight of wooden cylinder
=π(2r)2×h×ρ3×g
=π×4r2hρ3g
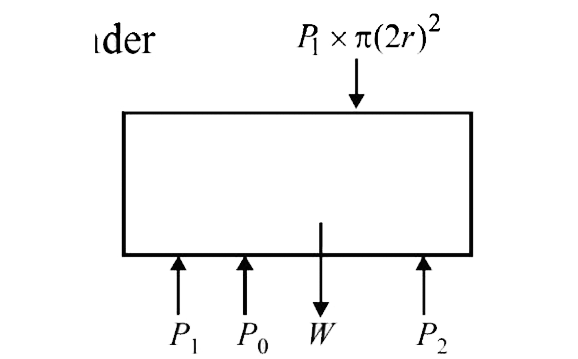
(b) Force due to pressure (P1) created by liquid of height h1 above the wooden block is
=P1×π(2r)2=[P0+h1ρg]×π(2r)2
=[P0+(h1+h)ρg]×π×3r2+P0πr2
At the verge of rising
[P0+(h1+h)ρg]×(π×3r2)+πr2P0
=[P0+h1ρg]×4πr2+π×4r2hρg3 or h1=5h3
Related Playlists
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems1videos
MECHANICAL PROPERTIES OF MATTER AND FLUIDS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced79videos
LAWS OF MOTION
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced30videos
MOMENTUM & IMPULSE
Similar Questions
A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, thenView SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
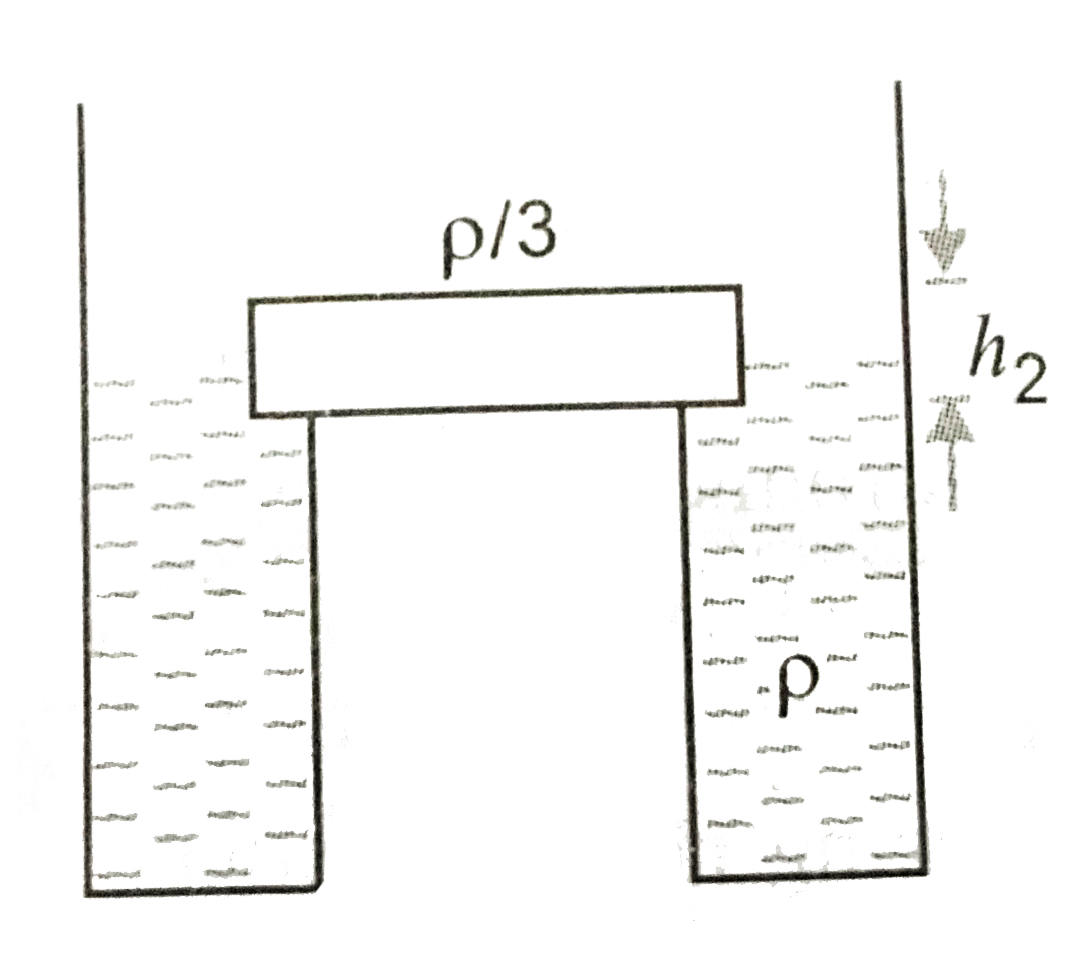
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceView SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If height h2 of water level is further decreased, thenView SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

The block in the above question is maintained by external means and the level of liquid is lowered. The height h2 when this external force reduces to zero is
 View Solution
View SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height h1 above the cylinder, the block just start moving up. Then the value of h1 isView SolutionA wooden cylindrical of diameter 4r, height h and density ρ/3 is kept on a hole of diameter 2r of a tank , filled with water of density ρ as shown in the figure . The height of the base of cylinder from the base of tank is H .
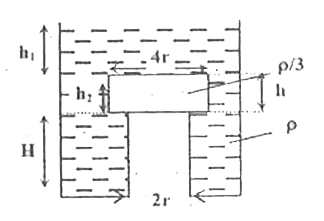
Let the cylinder is prevented from moving up , by applying a force and water level is further decreased . Then , height of water level (h2 in figure ) for which the cylinder remains in original position without application of force isView Solution
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.View SolutionA block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionAn open pan P filled with water (density ρm) is placed on one side of the pan as shown. If water depth is more then height of the block, then choose the correct statement.
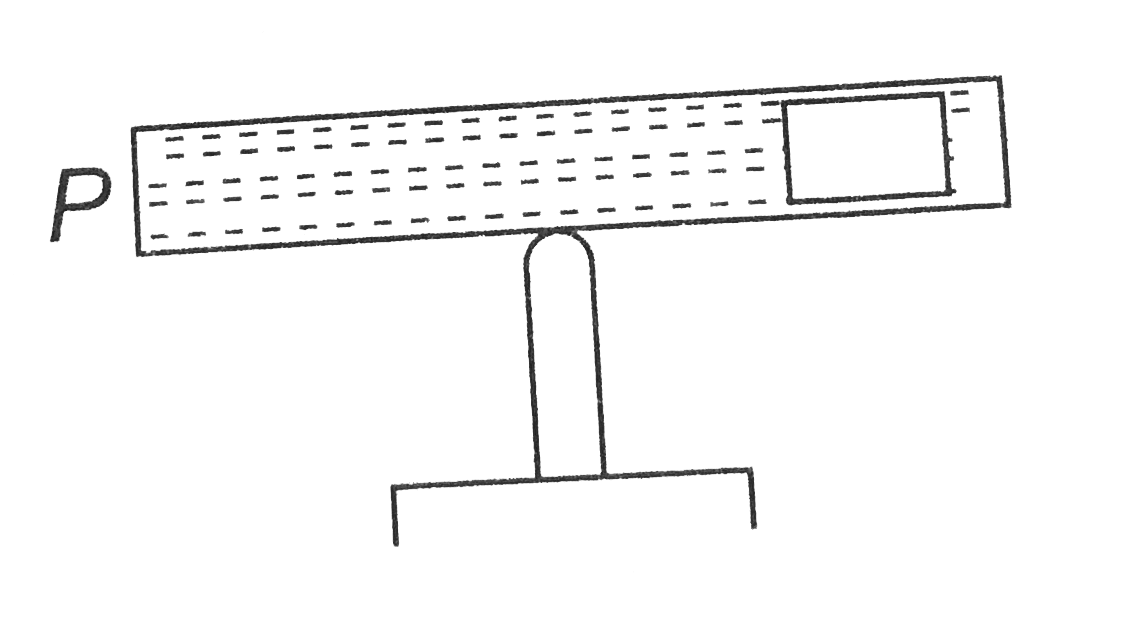 View Solution
View Solution


