A conductor with rectangular cross section has dimensions (a×2a×4a) as shown in fig.1.54 Resistance across AB is R1, across CD is R2 and across EF is R3. Then

R1=R2=R3
R1>R2>R3
R2>R3>R1
R1>R3>R2
The correct Answer is:D
R1=ρ(4a)(4a)(2a)=2ρa
R2=ρ(a)(4a)(2a)=ρ8a,
R3=ρ(2a)(4a)(a)
∴R1>R3>R2
Topper's Solved these Questions
- CURRENT ELECTRICITY Book:CHHAYA PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:EXERCISE ( VERY SHORT ANSWER TYPE QUESTION)
Explore 44 Videos
- CURRENT ELECTRICITY Book:CHHAYA PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:EXERCISE ( SHORT ANSWER TYPE QUESTION-I)
Explore 23 Videos
- CURRENT ELECTRICITY Book:CHHAYA PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:NCERT EXEMPLAR QUESTION WITH ANSWER HINT(MCQ-2)
Explore 1 Video
- COMMUNICATION STSTEMBook:CHHAYA PUBLICATIONChapter:COMMUNICATION STSTEMExercise:CBSE SCANNER
Explore 28 Videos
- DIFFRACTION AND POLARISATION OF LIGHTBook:CHHAYA PUBLICATIONChapter:DIFFRACTION AND POLARISATION OF LIGHTExercise:CBSE SCANNER
Explore 27 Videos
Similar Questions
Knowledge Check
A conductor with rectangular cross section has dimensions (a×2a×4a) as shown in figure. Resistance across AB is x, across CD is y and across EF is z. Then
 Ax=y=zBx>y>zCy>z>xDx>z>y
Ax=y=zBx>y>zCy>z>xDx>z>yIn the circuit shown in figure resistance of each wire is r. Net resistance across
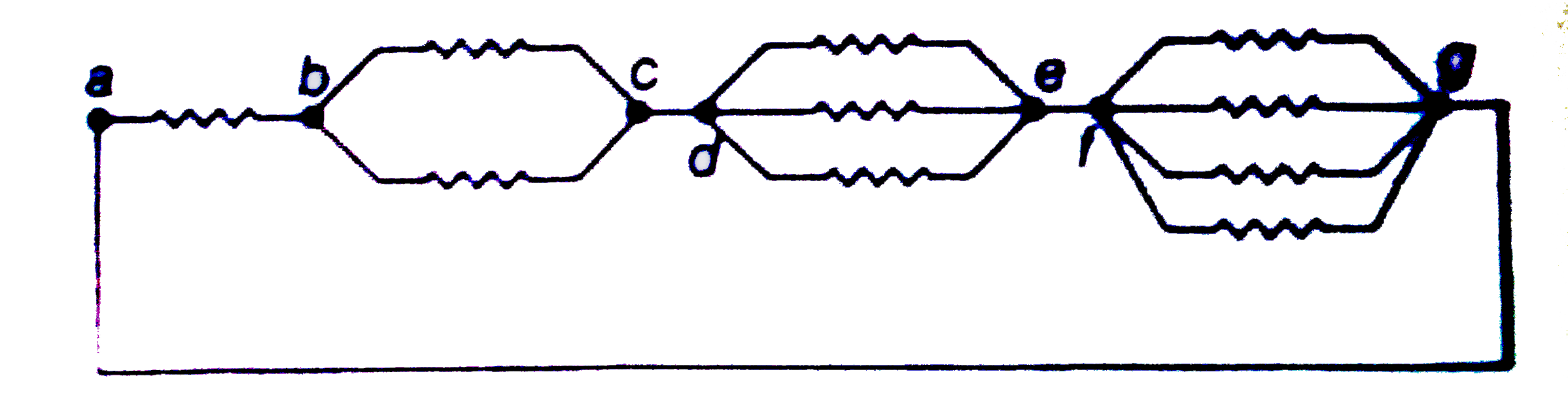 Aa and b is 1325rBb and c is 1950rCd and e is 725rDf and g is 1150r
Aa and b is 1325rBb and c is 1950rCd and e is 725rDf and g is 1150r
The dimensions of a conductor of specific resistance p are shown. Find the resistance of the conductor across AB, CD and EF.
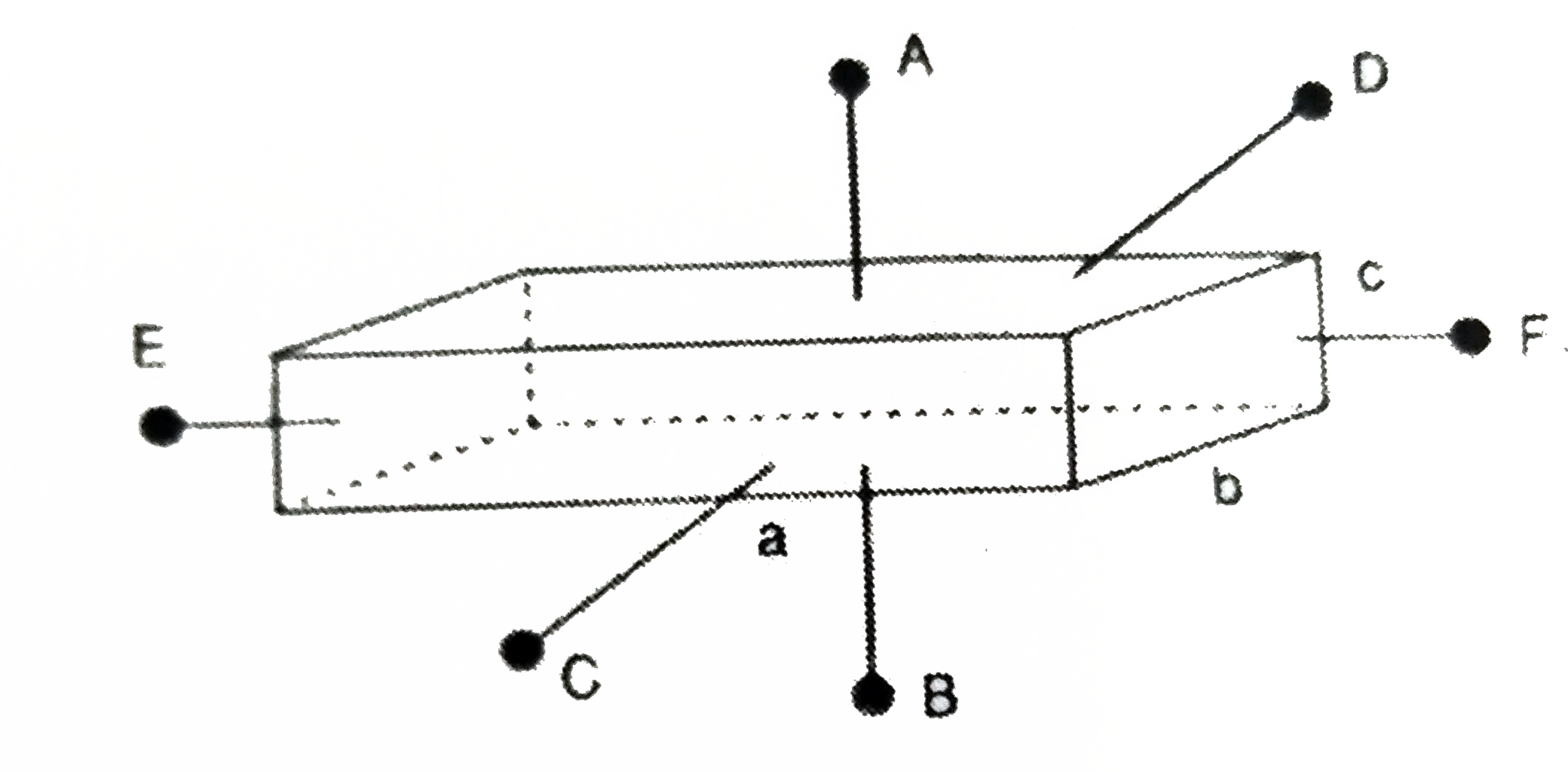
View SolutionThe dimensions of a conductor of specific resistance p are shown. Find the resistance of the conductor across AB, CD and EF.

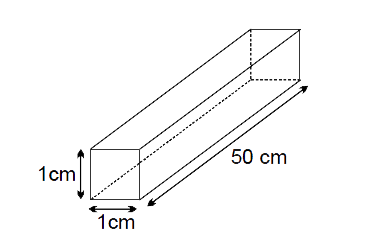
View SolutionA rectangular carbon block has dimensions 1.0 cm×1.0 cm×50 cm. Resistance are measured , first across two square ends and then across two respectivelt . If resistivity of carbon is 3.5×10−5Ω-m , then values of measured resistance respectively are :
View SolutionIn the circuit shown in figure resistance of each wire is r. Net resistance across

View SolutionA metallic conductor of irregular cross-section is as shown in the figure. A constant potential difference is applied across the ends (1) and (2). Then :

View Solution
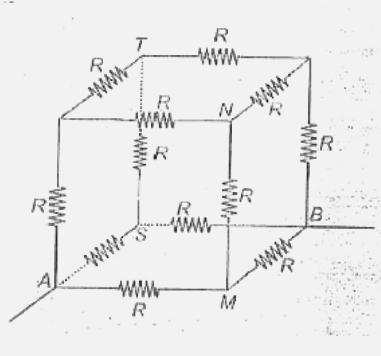
Tweve identical resistance each of resistance R are joined to form a cube as shown in figure.
Find resistance of the combination across AB
View Solution