A circular disc of moment of inertia is rotating in a horizontal plane about its symmetry axis with a constant angular velocity . Another disc of moment of inertia is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed . Calculate the energy lost by the initially rotating disc due to friction.
Here,
Let be the initial angular speed
Let be the final angular speed of the system.
According to the law of conservation of angular momentum,
..(i)
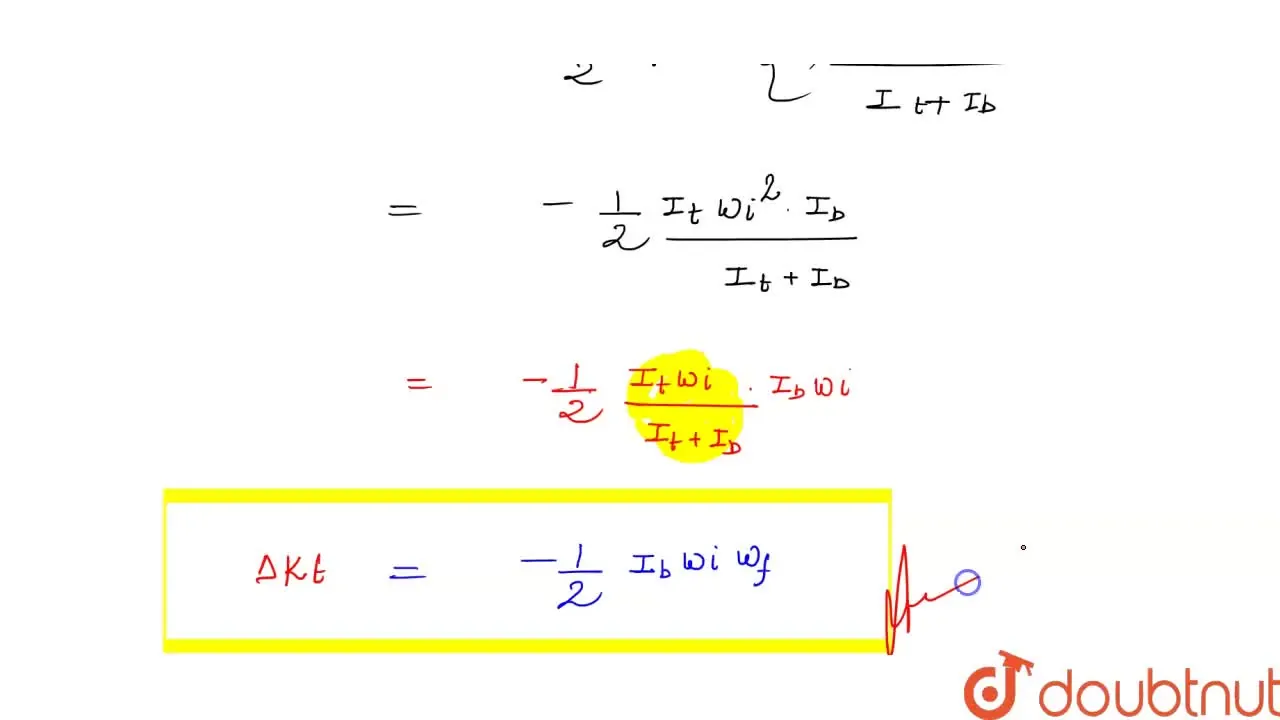
Energy lost
using (i),we get
Energy lost
Energy lost [using (i)]
Related Playlists
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE B2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE C2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE A2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A circular disk of moment of inertia It is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disc to friction is
View SolutionA disc of the moment of inertia 'l1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1' . Another disc of moment of inertia 'I2'. having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is
View SolutionA disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
View SolutionA thin and circular disc of mass m and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . If another disc of same dimension but mass ml4 is placed gently on the first disc co-axially, then the new angular velocity of the system is
View SolutionA disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to the plane at an angular velocity ω . Another disc of mass M / 3 but same radius is placed gently on the first disc coaxially . the angular velocity of the system now is
View SolutionA uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity ω. Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity ω. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed ofthe composite disc will be:
View Solution