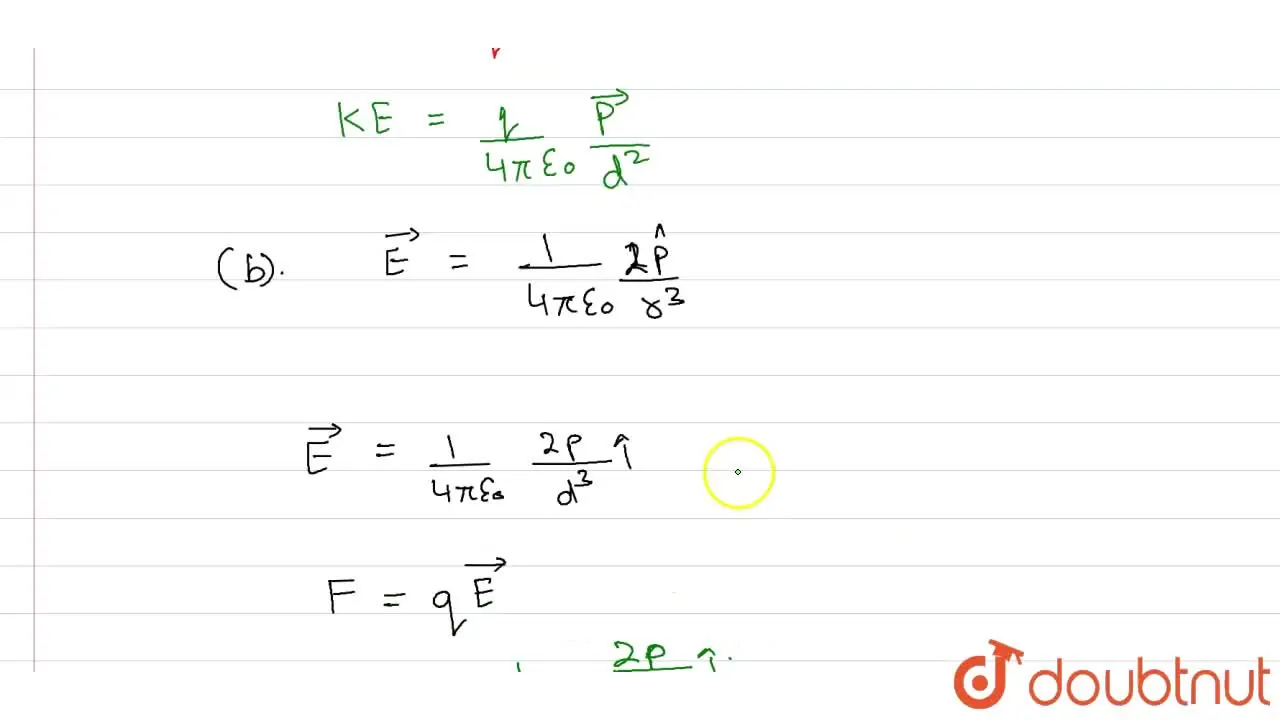
A charge is fixed at the origin of the co-ordinate system while a small electric dipole of dipolement pointing away from the charge along the x-axis is set free from a point far away from the origin.
(a) Calculate the K.E. of the dipole when it reaches to a point (d, 0).
(b) Calculate the force on the charge at this moment.

Conserving energy (fig)
constant
or
or
Force on dipole
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Interger Answer type20videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks10videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A positive point charge q is fixed at origin. A dipole with a dipole momen →p is placed along the x-axis for away from the orgin with →p poiniting along positive x-axis .
(i) If the kinetic energy of the diople when it reachers a distance d from the origin is qp4πε0dn, then n is .
(ii) If the force experienced by the charge q at this moment is 4qpπε0d3,ˆi then x is.View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View SolutionThe electric field of an electric dipole at a point on its axis , at a distance d from the centre of the dipole, varies as
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will beView SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
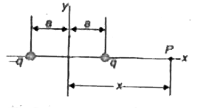
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .View SolutionAn electric dipole is fixed at the origin of coordinates. Its moment is directed in the positive x- direction. A positive charge is moved from the point (r,0) to the point (−r,0) by an external agent. In this process, the work done by the agent is
View Solution