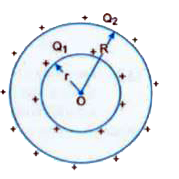
A charge Q is distributed over the surfaces of two concentric hollow spheres of radii r and $R (R > > r)$ , such that their surface charge densities are equal . Derive the expression for the potential at the common centre.

Text Solution

Verified by Experts

As shown let charges on inner and outer spheres be $Q_{1}$ and $Q_{2}$ respectively , where $Q_{1} + Q_{2} = Q$
Let common surface charge density be $σ$ , then
$Q_{1} = 4 π r^{2} σ$ and $Q_{2} = 4 π R^{2} σ$
$\Rightarrow Q = Q_{1} + Q_{2} = [4 π r^{2} + 4 π R^{2}] σ = 4 π σ [r^{2} + R^{2}] \Rightarrow σ = \frac{Q}{4 π [r^{2} + R^{2}]}$
Thus , $Q_{1} = \frac{4 π r^{2} \cdot Q}{4 π [r^{2} + R^{2}]} = \frac{Q r^{2}}{(r^{2} + R^{2})}$ and $Q_{2} = \frac{4 π R^{2} \cdot Q}{4 π [r^{2} + R^{2}]} = \frac{Q R^{2}}{(r^{2} + R^{2})}$
Now potential at centre point O due to charge $Q_{1}$ on the hollow sphere of radius r is , $V_{1} = \frac{Q_{1}}{4 π \in_{0} r} = \frac{Q r^{2}}{4 π \in_{0} r (r^{2} + R^{2})} = \frac{Q r}{4 π \in_{0} (r^{2} + R^{2})}$
and potential at centre point O due to charge $Q_{2}$ on the hollow sphere of radius R is , $V_{2} = \frac{Q_{2}}{4 π \in_{0} R} = \frac{Q R^{2}}{4 π \in_{0} R (r^{2} + R^{2})} = \frac{Q . R}{4 π \in_{0} (r^{2} + R^{2})}$
$∴$ Total potential at centre point O
$V = V_{1} + V_{2} = \frac{Q r}{4 π \in_{0} (r^{2} + R^{2})} + \frac{Q . R}{4 π \in_{0} (r^{2} + R^{2})} = \frac{Q}{4 π \in_{0}} \cdot \frac{(r + R)}{(r^{2} + R^{2})}$

Updated on:21/07/2023