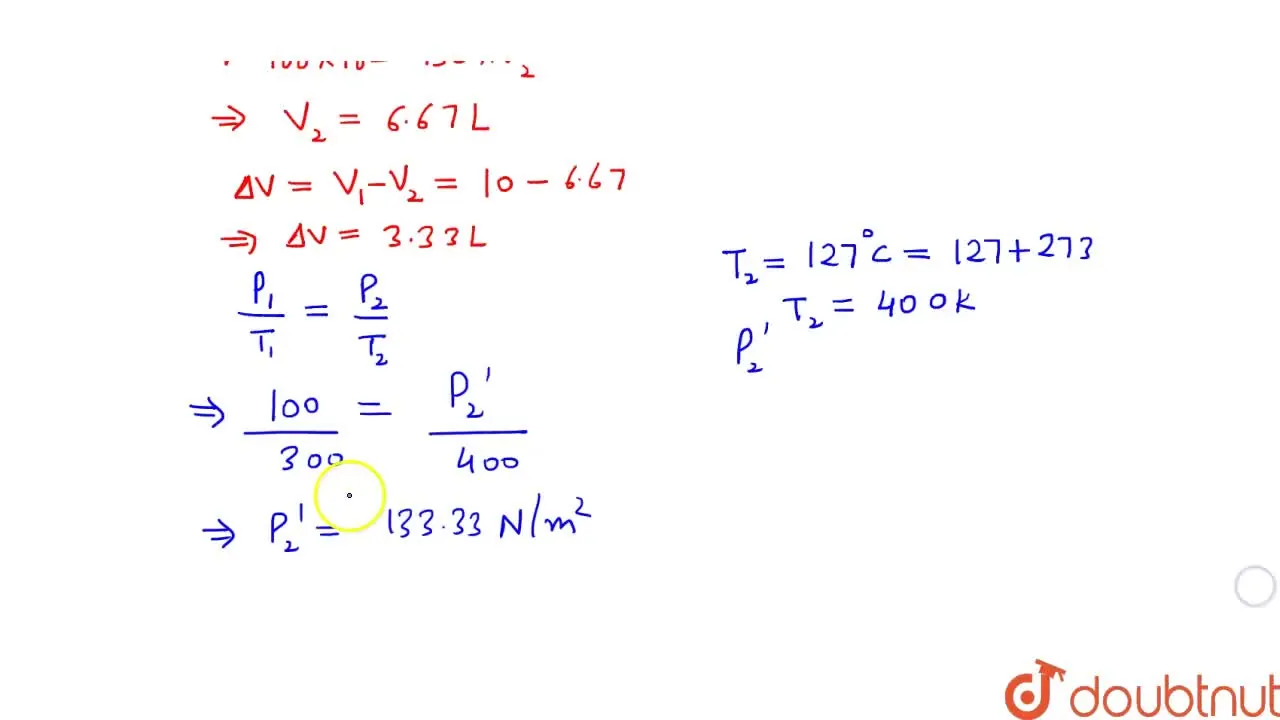A certain mass of gas in a cylinder at 27∘C has a volume of 10 litre and pressure 100 N/m2. (i) The gas is first compressed at constant temperature and the pressure is raised to 150 N/m2 . Find the change in volume. (ii) If the gas is then heated at constant volume and if the temperature is raised to 127∘C, find the new pressure.
T1=27+273=300K,V1=10l,P1=100N/m2
(i) The gas is compressed at constant temperature
P2=150N/m2,V2=?
P1V1=P2V2
V2=P1V1P2=100×10150=6.67l
Change in volume =V1−V2=10−6.67=3.33l
(ii) The gas is heated at constant volume
T2=127+273=400K,P2=?
P1T1=P2T2,P2=P1T2T1=100×400300=133.33N/m2
Related Playlists
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 (SOLVED EXAMPLES)11videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)2videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2 (SOLVED EXAMPLES)22videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D12videos
SAMPLE QUESTION PAPER - 01
Similar Questions
A gas at 27∘C in a cylinder has a volume of 4 litre and pressure 100Nm−2.
(i) Gas is first compressed at constant temperature so that the pressure is 150Nm−2 . Calaulate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes 127∘C. Calculate the new pressure.View SolutionA gas at 27∘C in a cylinder has a volume of 4 litre and pressure 100Nm−2.
(i) Gas is first compressed at constant temperature so that the pressure is 150Nm−2 . Calculate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes 127∘C. Calculate the new pressure.View SolutionThe pressure of a given mass of a gas contained in a vessel at constant temperature is reduced to half. Calculte the change in volume of the gas
View SolutionOne mole of a gas is heated at constant pressure to raise its temperature by 1∘C. The work done in joules is
View Solution120 cm3 of a gas is taken at 27.3 K. The temperature is then raised to 0∘C What is the new volume of the gas ? The pressure is kept constant.
View SolutionA gas at 240 K is heated to 127∘C . Find the percentage change in the volume of the gas (pressure remaining constant)
View SolutionThe percentage change in the pressure of gas at constant temperature is 200% (increases). Calculate the percentage change in the volume of the gas.
View SolutionPressure of a gas at S.T.P. is doubled and the temperature is raised to 546 K. What is the final volume of the gas ?
View SolutionOne litre of a gas at 10∘C is heated till both its volume and pressure are tripled. Find the new temperature.
View SolutionA certain amount of a gas at 27∘C and 1 atmospheric pressure occupies a volume of 25dm3. If the pressure is kept constant and the temperature is raised to 77∘C, what would be the volume of the gas ?
View Solution