A box P and a coil Q are connected in series with an AC source of variable frequency.The EMF of source is constant at 10V.Box P contains a capacitance of 1μF in series with a resistance of 32Ω.Coil Q has a self inductance 4.9mH and a resistance of 68Ω.The frequency is adjusted so that the maximum current flows in P and Q.Find the impedance of P and Q at this frequency.Also find the voltage across P and Q respectively.
The correct Answer is:P=76.96Ω,Q=97.59Ω,P=7.6V;Q=9.8V, net impedance=100Ω
Here L=4.9mH
C=1μF
R=68+32=100Ω
ω=1√LC=17×105rad/sec
ZP=√(32)2+(1/ωC)2=76.96Ω
ZQ=√(68)2+(ωC)2=97.59Ω
Total imedence Z=√R2+(XL−XC)2
=√1002+(1057×4.9×10−37×10−510−6)=100Ω
Irms=10100A
VP=ZP×Irms=7.7V
VQ=ZQ×Irms=9.8V
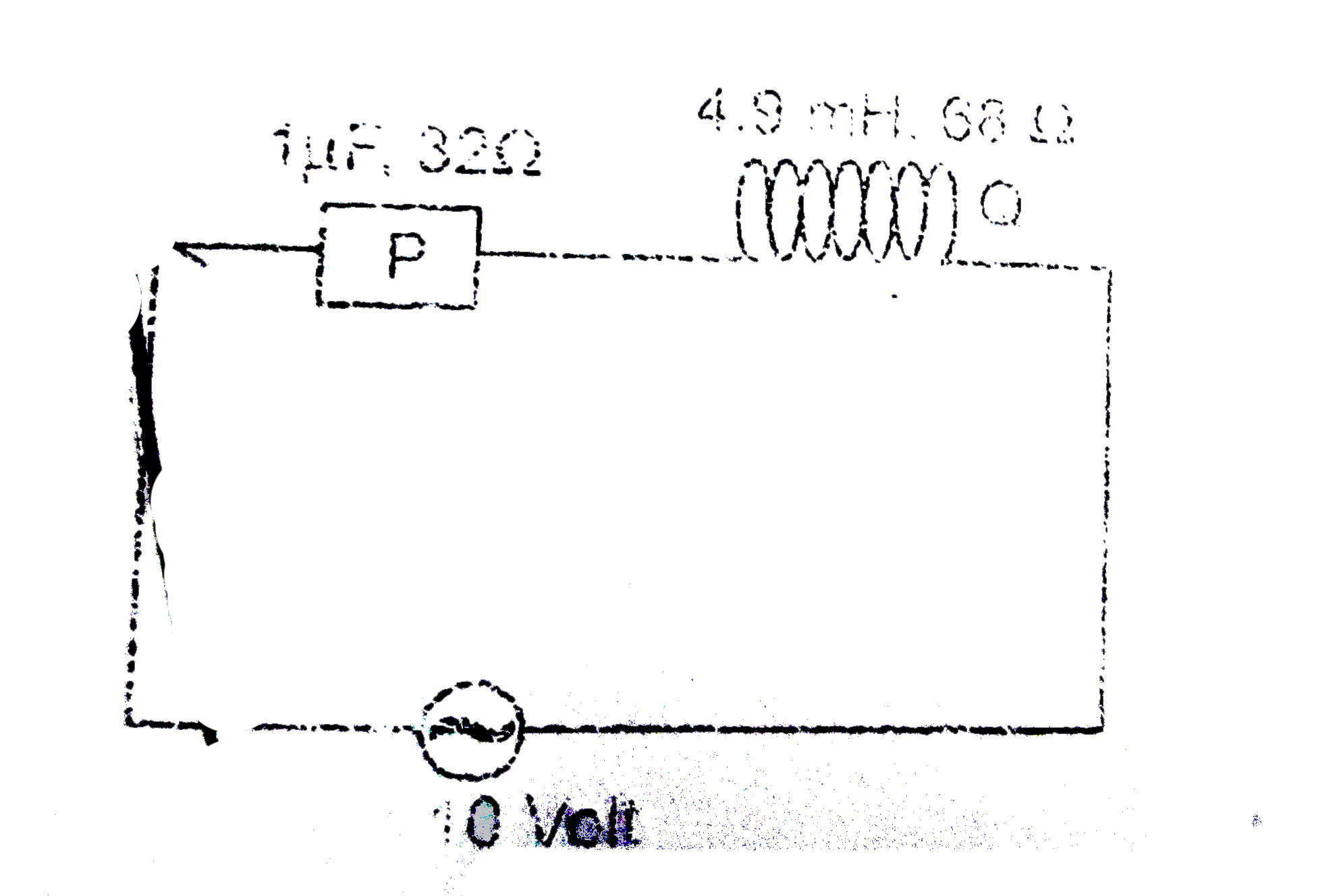
Related Playlists
- BOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - SOLVED MISCELLANEOUS14videos
ALTERNATING CURRENT
- BOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE SECTION A4videos
ALTERNATING CURRENT
- BOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -3 Part-324videos
ALTERNATING CURRENT
- BOOK - RESONANCECHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
Similar Questions
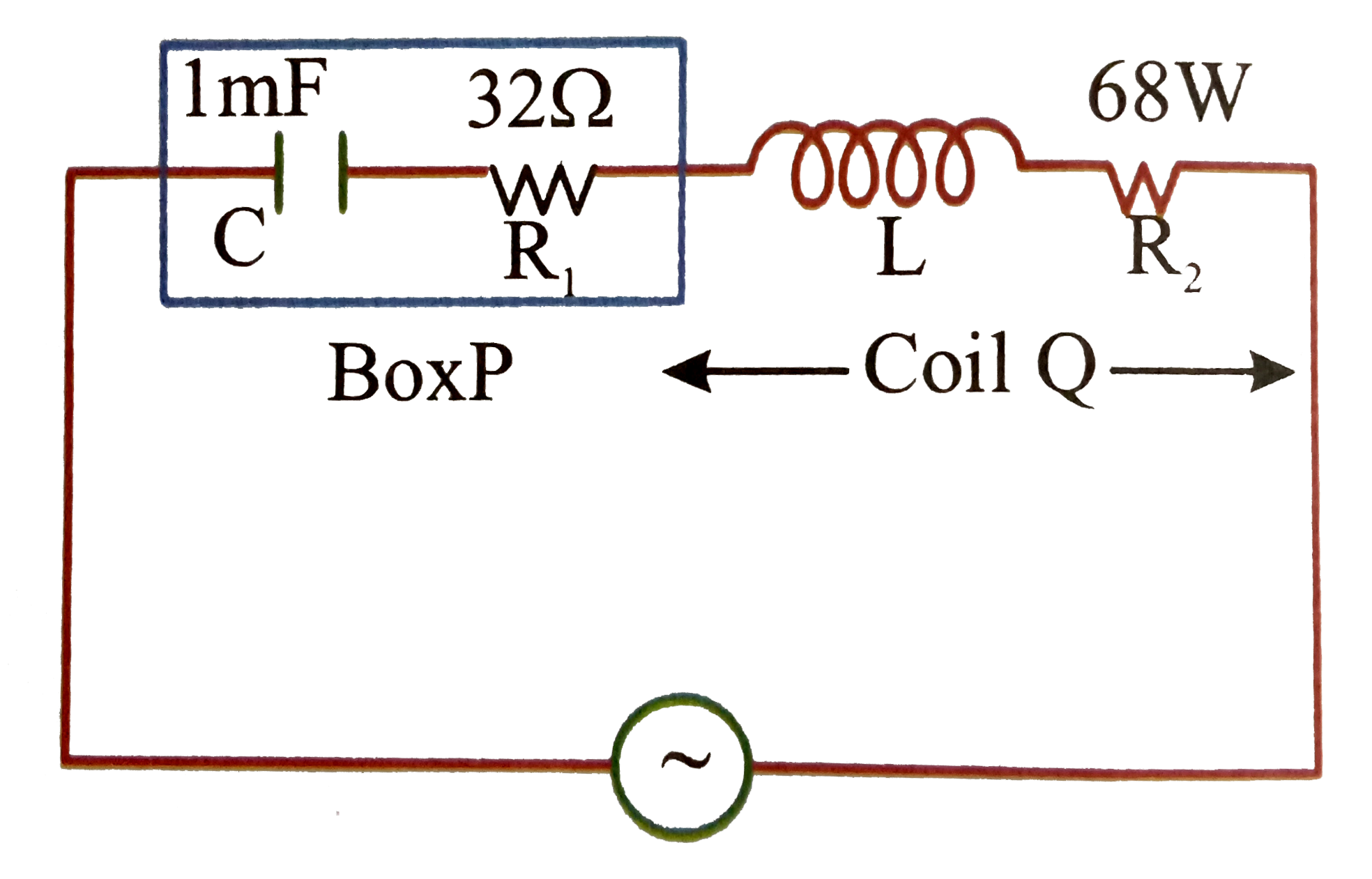
A box P and a coil Q are connected in series with an AC source of variable frequency. The emf of the source is constant at 10V. Box P contains a capacitance of 1μF in series with a resistance of 32Ω. Coil Q has a self-inductance 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted to that the maximum current flows in P and Q. At this frequency
(a) The impedance of P is 77Ω
(b) The impedance of Q is 85Ω
(c ) Voltage across P is 7.7V
(d) Voltage across Q is 9.7V
 View Solution
View SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P xontains a capacitance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
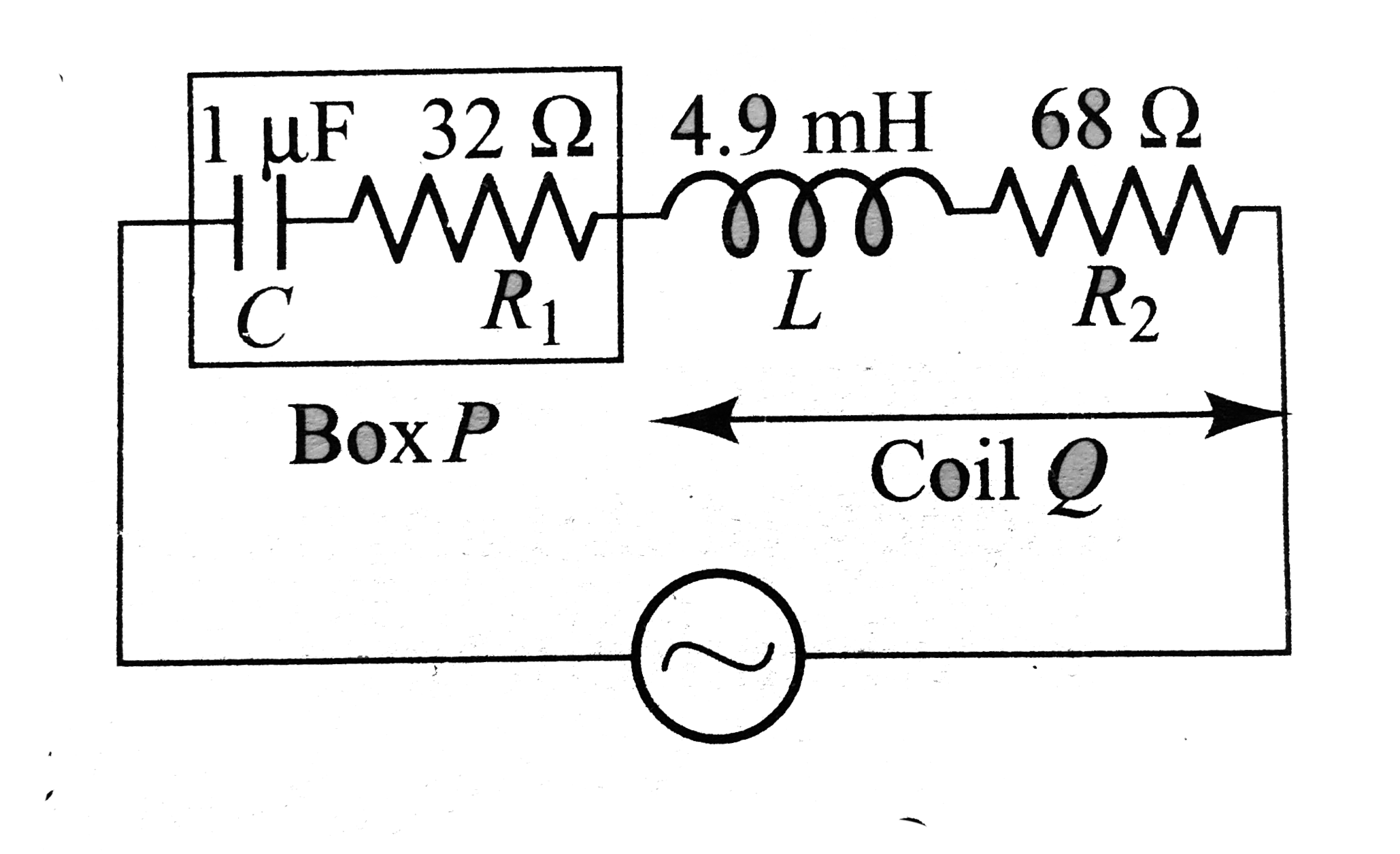
The impedance of P at this frequency isView SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P xontains a capacitance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
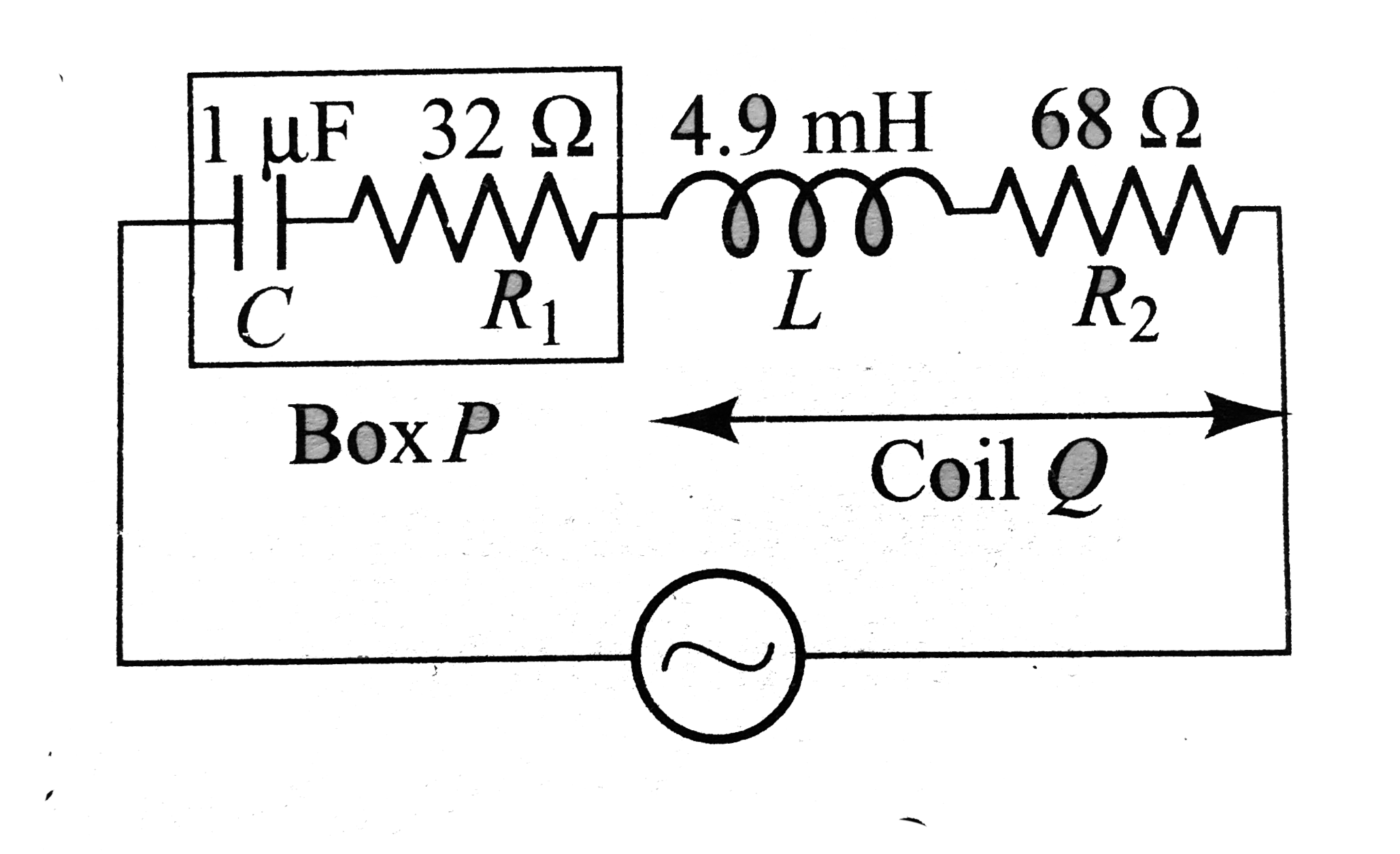
The impendance of Q at this frequency isView SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P xontains a capacitance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.

the voltage across Q isView SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P xontains a capacitance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
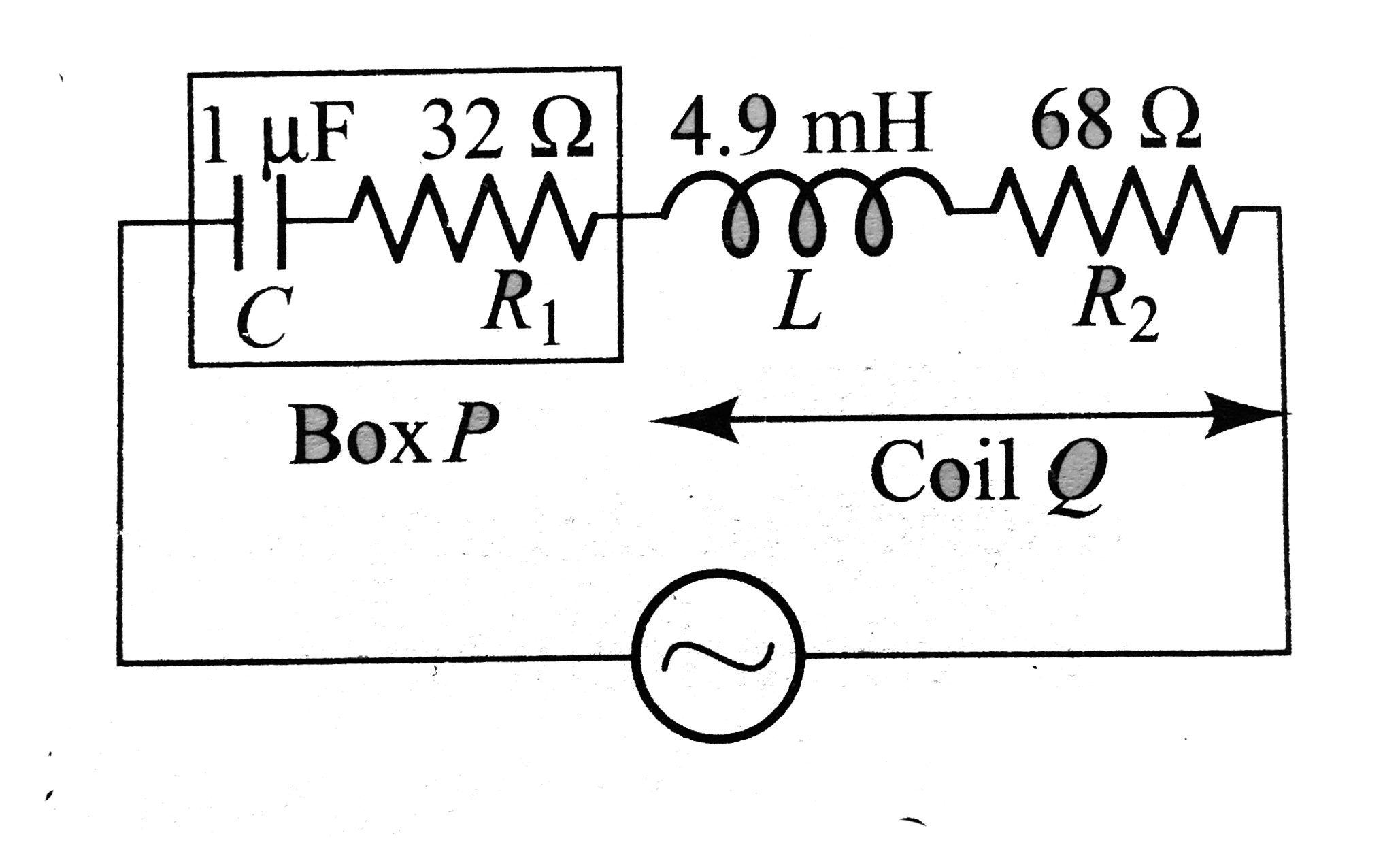
The voltage across P isView SolutionIt is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
Impedance of box P at the above frequency isView SolutionIt is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
Power factor of the circuit at maximum current isView SolutionIt is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
The angular frequency foer which he detects maximum current in the circuit isView SolutionA box P and a coil Q are connected in series with an ac source of variable freguency The emf of the source is constant at 28V The frequency is so adjusted that the maximum current flows in P and Q Find
(a) impedance of P and Q at this frequency
(b) voltage across P and Q
 .View Solution
.View SolutionFind the resonant frequency of a series circuit consist of an inductance 200 μH, a capacitance of 0.0005μF and a resistance of 10 Ω.
View Solution


