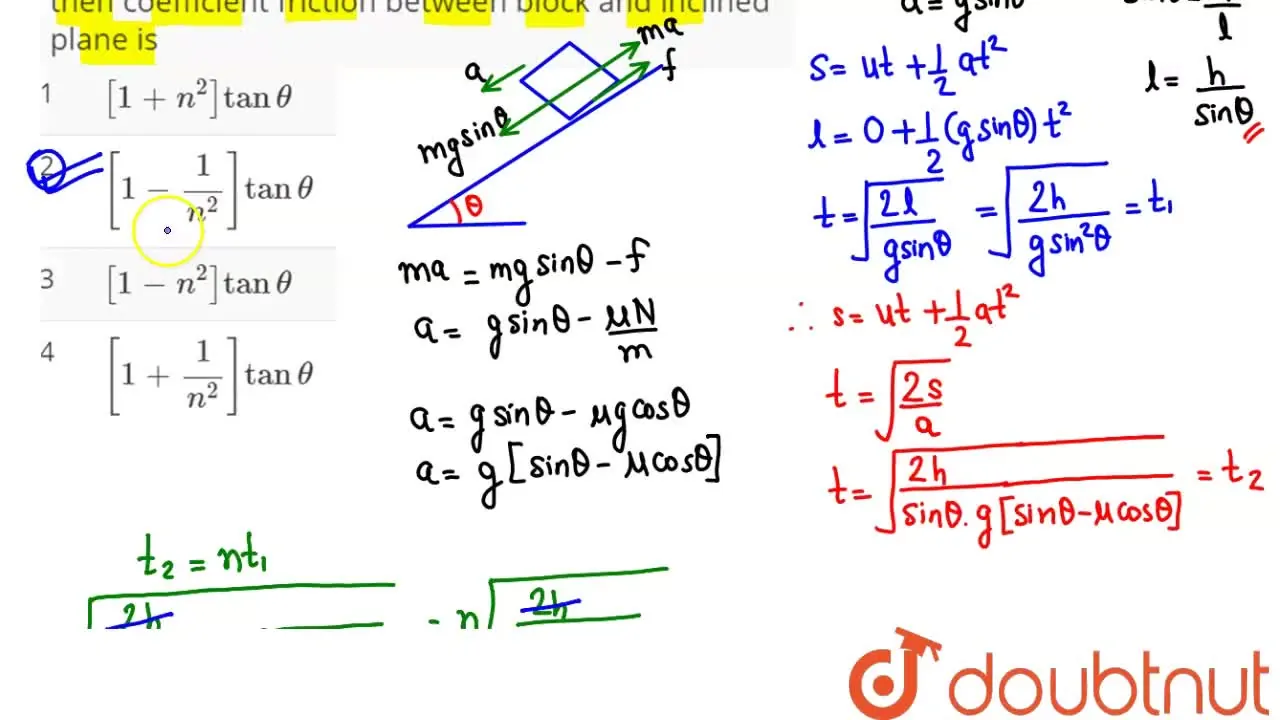
A block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
[1+n2]tanθ
[1−1n2]tanθ
[1−n2]tanθ
[1+1n2]tanθ
Step by step video & image solution for A block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination theta and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)63videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)15videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)65videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
Similar Questions
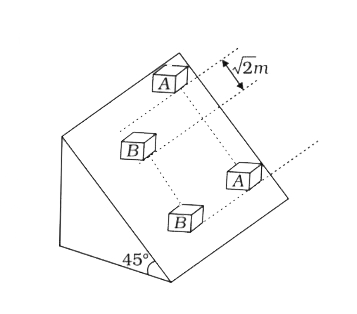
Two identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
 View Solution
View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2
 View Solution
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction
 View Solution
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
 View Solution
View SolutionA block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :
 View Solution
View SolutionStarting from rest, a body slides down a 45∘ inclined plane in twice the time it itakes to slide the same distance in the absence of friction.
They the coefficient of friction between the body and the inclined plane isView SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution