A beam of plane polarised light of large cross - sectional area and uniform intensity of 3.3Wm−2 falls normally on a polariser (cross sectional are 3×10−4m2 ) which rotates about its axis with an angular speed of 31.4 rad/s . The energy of light passing through the polariser per revolution , is close to :
1.5×10−4J
5.0×10−4J
1.0×10−4J
1.0×10−5J
Step by step video & image solution for A beam of plane polarised light of large cross - sectional area and uniform intensity of 3.3Wm^(-2) falls normally on a polariser (cross sectional are 3xx10^(-4)m^2 ) which rotates about its axis with an angular speed of 31.4 rad/s . The energy of light passing through the polariser per revolution , is close to : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
A beam of plane polarized light having flux 10−3 Watt falls normally on polarizer of cross sectional area 3×10−4m2. Polarizer rotates with angular frequency of 31.4 rad/s. Energy of light passes through the polarizer per revolution will be
View SolutionA uniform circular disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the kinetic energy of the disc and its angular momentum about the axis of rotation.
View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
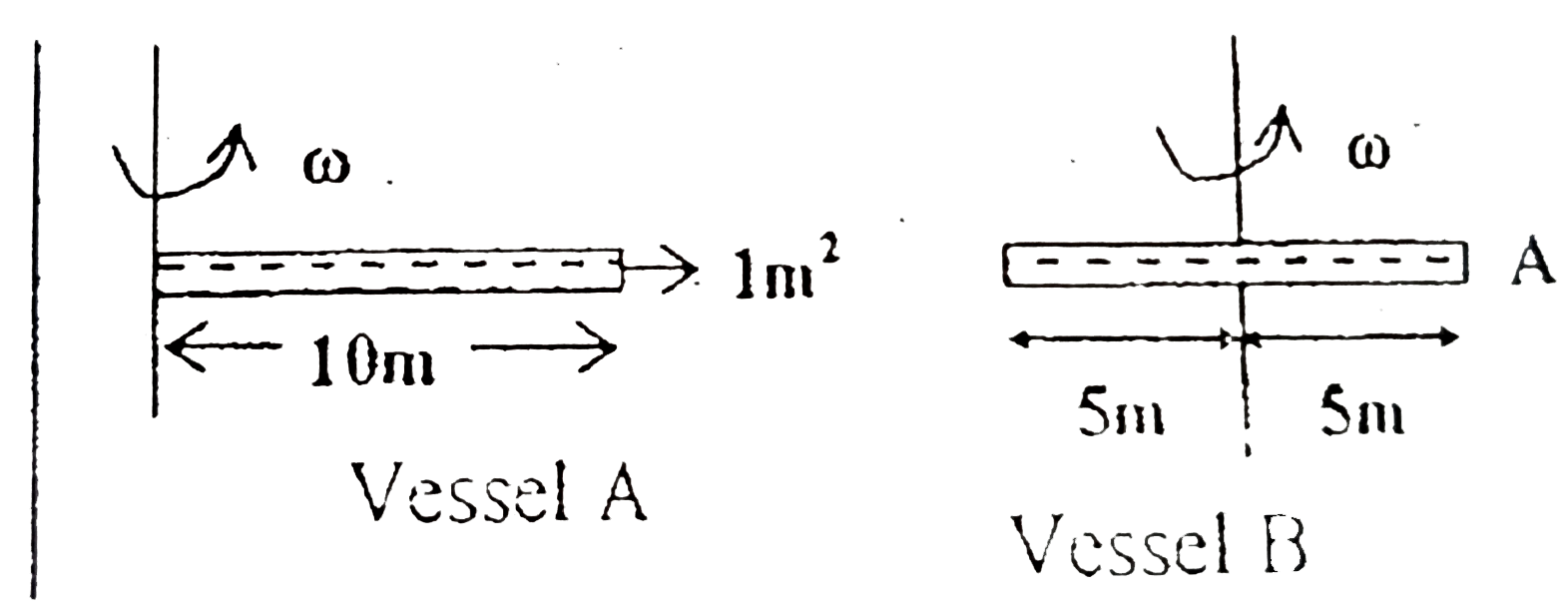 View Solution
View SolutionIf 106 electrons/s are flowing through an area of cross section of 10−4m2 then the current will be:-
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionA flywheel having a radius of gyration of 2m and mass 10 kg rotates at an angular speed of 5rads−1 about an axis perpendicular to it through its centre. The kinetic energy of rotation is
View SolutionA straight solenoid of length 50 cm has 1000 turns per metre and mean cross-sectional area of 2×10−4m2 . It is placed with its axis of 30∘ with uniform magnetic field of 0.32 T . Find the torque acting on the solenoid when a current of 2 ampere is passed through it .
View SolutionA body rotates about a fixed axis with an angular acceleration of 3rad/s2 . The angle rotated by it during the time when its angular velocity increases frm 10 rad/s to 20 rad/s (in radian) is
View SolutionA wire 4 m long and cross section 3×10−6m2is stretched by Imm. If its Young.s modulus is 2×1011N/m2, find the energy stored in the wire.
View SolutionA solenoid of cross-sectional area 2×10−4m2 and 900 turns has 0.6Am2 magnetic moment. Then the current flowing through it is
View Solution


