A battery of 3.0 V is connected to a resistor dissipating 0.5 W of power . If the terminal voltage of the battery is 2.5 V , the power dissipated within the internal resistance is :
0.072 W
0.125 W
0.50 W
0.10 W
Step by step video & image solution for A battery of 3.0 V is connected to a resistor dissipating 0.5 W of power . If the terminal voltage of the battery is 2.5 V , the power dissipated within the internal resistance is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If the power dissipated in 5Ω is 20 W then power dissipated in 4Ω is -
 View Solution
View SolutionA high resistance voltmeter measures the potential difference across a battery to be 9-0 V. On connecting a 24 2 resistor across the terminals of the battery, the voltmeter reads 7.2 V. Calculate the internal resistance of the battery.
View SolutionA battery of emf 10 V is connected with a load resistance of 50 Omega the total power delivered by the battery is 2 W. If load resistance is replaced by R then power delivered is 4 W, the value of R is
View SolutionIn an AC circuit with voltage V and current I, the power dissipated is
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionPower dissipated across the 8Ω resistor in the circuit shown here is 2 w. The power U dissipated in watt units across the 3Ω resistor is .
View SolutionA current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
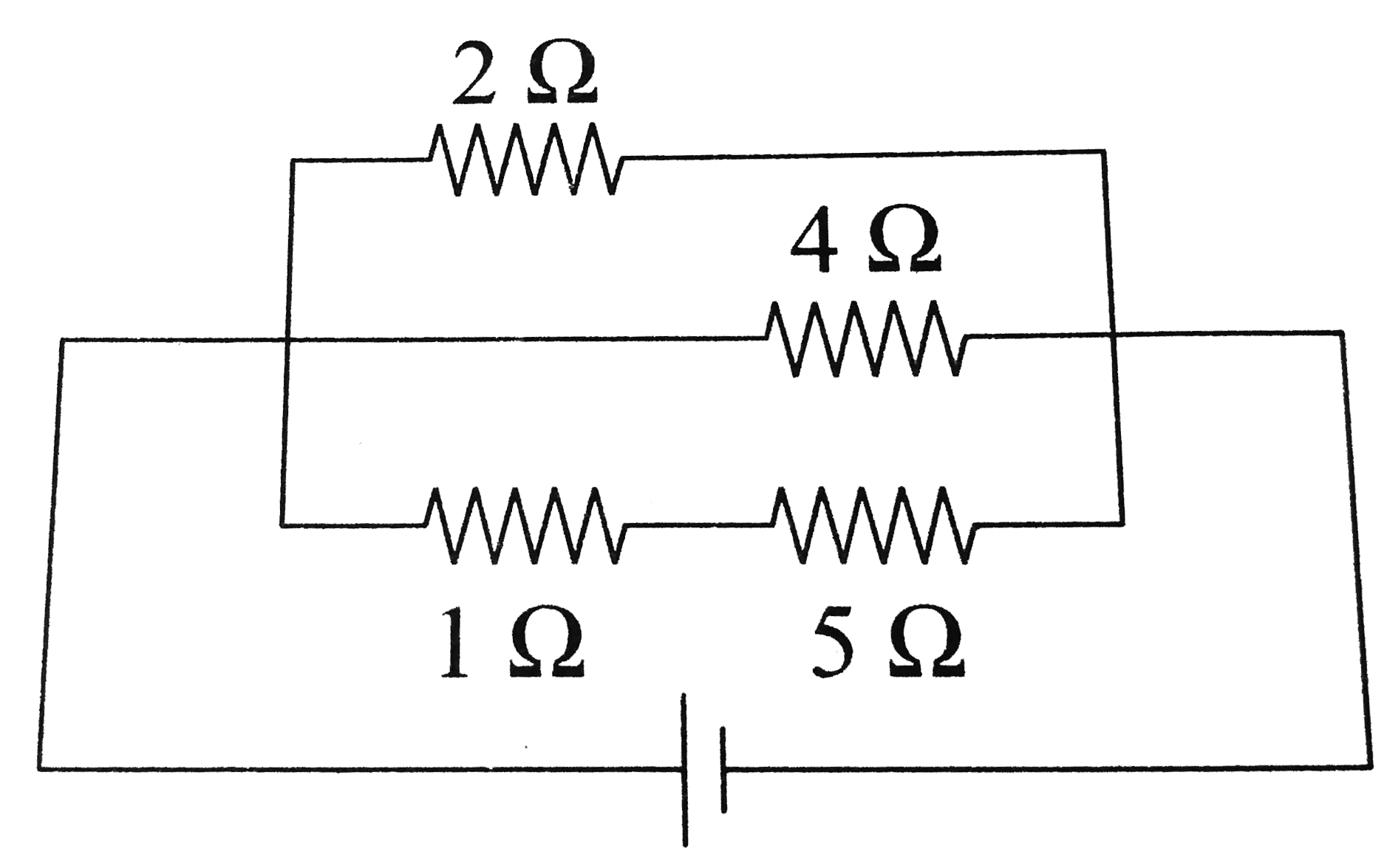 View Solution
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
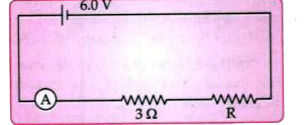
Calculate the power dissipated in the 3Ω resistor.View Solution


