(a) A particle is moving eastward with a velocity of 5 m/s. If in 10 s the velocity changes by 5m/s northwards. What is the average acceleration in this time ?
(b) What is the retardation of a moving particle if the relation between time and position is, t=Ax2+Bx? (where A and B are appropriate constants)
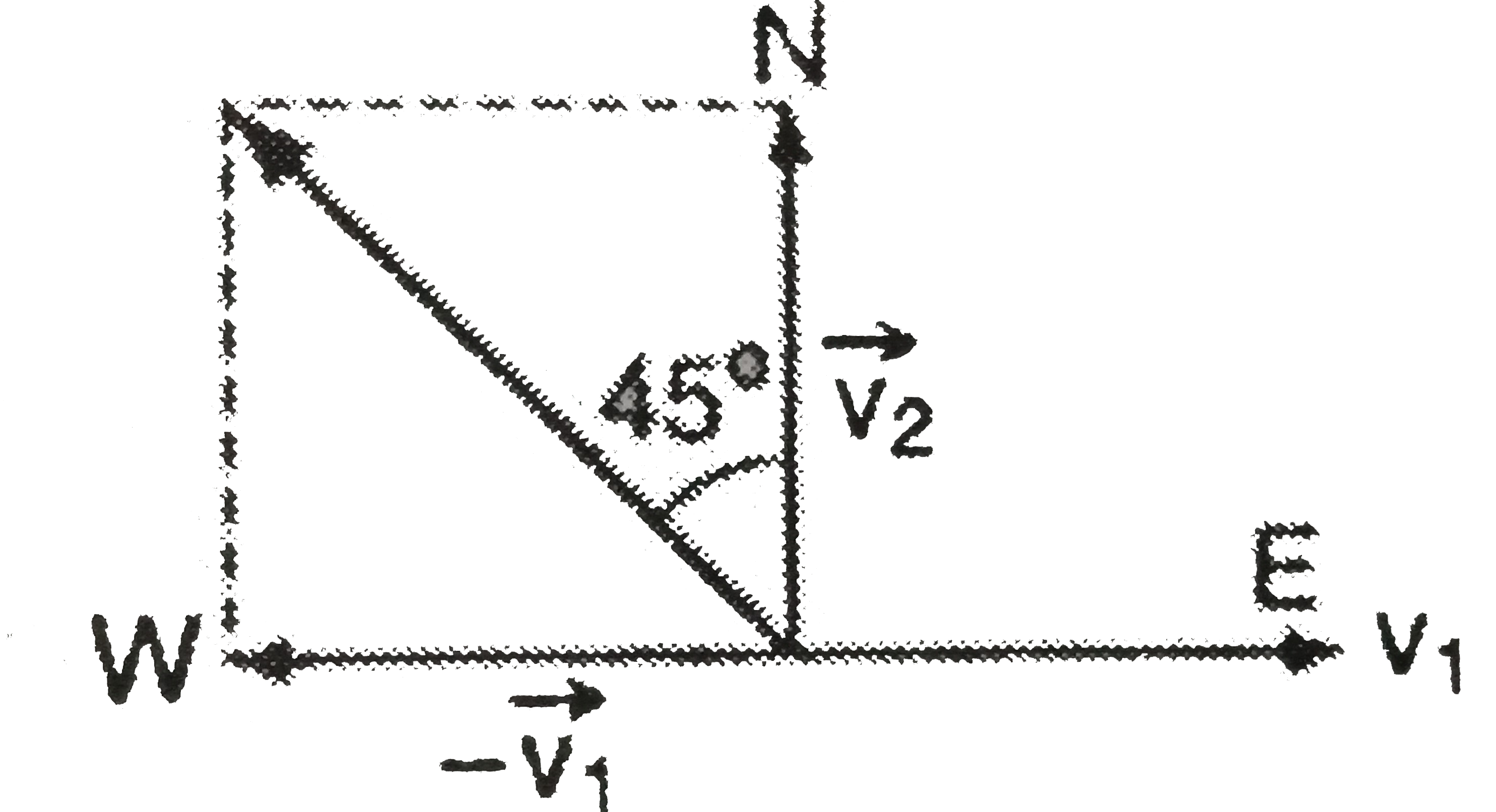
Δ→v2−→v1=→v2+(−→v1)
i.e., Δ→v=(√52+52)N−W
i.e., Δ→v=5√2N−W
So, →aav=Δ→vΔt=5√210N−W
i.e., →aav=1√2(m/s2)N−W
(b) As t=Ax2+Bx
So, dtdx=2Ax+B or v=(2Ax+B)−1...(i)
Now by chain rule,
a=dvdt=dvdx.dxdt=vdvdx [as dxdt=v]
So, a=vddx(2Ax+B)−1 [from Eqn. (i)]
or a=v(−1)(2Ax+B)−2(2A)
or a=−2A(2Ax+B)−3 [as v=(2Ax+B)−1]
So, retardation =−a2A(2Ax+B)−3
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Problem
Explore 14 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Problems and Practice
Explore 16 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:GRB PUBLICATIONChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:All Questions
Explore 210 Videos
Similar Questions
A paricle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s northwards. Find the average acceleration in this time.
View SolutionA particle is moving eastward with a velocity of 5m/s in 10 s the velocity changed by 5m/s northwards.The change in velocity is
View Solution
Knowledge Check
The retardation fo a moving particle if the relation between time and position is t=Ax3+Bx2 where A and B are appropriate constants will be .
A(a)6Ax+2B(3Ax2+2Bx)3B(b) (6Bx+6A)/((3 Ax^2 + 2 B x)^3)C(c ) 6A+2Bx(3Ax+2Bx2)3D(d) (6 A+2 B x)/( (3 A+ 2 B x^3)^2)A particle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s nothwards. The average acceleration in this time is
AzeroB1/√2m/s2 towards no rth - westC1/√2m/s2 towards no rth - eastD1/2m/s2 towards no rth - westA particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
AZeroB1√2m/s2 toward north-westC1√2m/s2 toward north-eastD12m/s2 toward north-west
A particle is moving eastwards with a velocity of 5ms−1. In 10seconds the velocity changes to 5ms−1 northwards. The average acceleration in this time is
View SolutionA particle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s nothwards. The average acceleration in this time is
View SolutionA particle is moving eastwards with a velocity of 5ms−1. In 10seconds the velocity changes to 5ms−1 northwards. The average acceleration in this time is
View SolutionA car is moving eastward with velocity 10 m/s. In 20 sec, the velocity change to 10 m/s northwards. The averge acceleration in this time.
View SolutionA particle is moving with velocity 5 m/s towards cast and its velocity changes to 5 m/s north in 10 s, find the acceleration .
View Solution

