The reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
Let the equilibrium constant of Step I be 2×10−3mol−1L and the rate constants for the formation of A2X and A2 in Step II and III are 3.0×10−2mol−1L−1min and 1×103mol−1L−1min (all data at 25∘C), then what is the overall rate constant (mol−2L2−1min) of the consumption of B2?
6×10−5
1.2×10−4
3×10−5
1.5×10−5
The correct Answer is:B
Rate of overall reacation =Rate of step II
(+d[N2O]dt)=kII[A2X2][B2]
form equilibrium step, i.e., step I
kc=[A2X2][AX]2,kc= equilibrium constant of step I
[A2X2]=kc[AX]2
(kII= rate of constant of formation of A2X)
=k[AX]2[B2]
k=Rate constant of overall reacation
Since for the rate of A2X consumed 2mol of B2 are formed so rate constant for the consmption of B2 will twice that of overall rate constant, i.e., 2kIIkc
2×3×10−2×2×10−3=1.2×10−4mol−2L2−1min
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct33videos
CHEMICAL KINETICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Single Correct177videos
CHEMICAL KINETICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex4.4 Objective10videos
CHEMICAL KINETICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)34videos
CARBOXYLIC ACIDS AND THEIR DERIVATIVES
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective18videos
COORDINATION COMPOUNDS
Similar Questions
The reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
How many times the rate of formation of A2 will increase if concentrations of AX is doubled and that of B2 is increased theee fold?View Solution2 is the equilibrium constant for the reaction A2+B2⇔2AB at a given temperature. What is the degree of dissociation for A2 or B2
View Solution
Knowledge Check
- Question 1 - Select One
The reaction ,2AB(g)+2C(g)→A2(g)+2BC(g) proceeds according to the mechanism .
I. 2AB⇔A2B2 (fast)
II. A2B2+C→A2B+BC (slow )
III. A2B+C→A2+BC (fast)
what will be the initial rate taking [AB] = 0.2 M and [C] = 0.5 M ? The Kc for the step I is 102M−1 and rate constant for the step II is 3.0×10−3mol−1−1minA0.0716M−1minB0.0891M−1minC0.006M−1minD0.0257M−1min
The gaseous reaction A(g)+B(g)⇔2C(g)+D(g)+q kJ is most favoured at :
View SolutionIn a reaction A2(g)+4B2(g)⇔2AB4(g),ΔH<0. The formation of AB4 is not favoured by
View SolutionThe equilibrium constant for the reaction
A2(g)+B2(g)⇔2AB(g)
is 20 at 500K. The equilibrium constant for the reaction 2AB(g)⇔A2(g)+B2(g) would beView SolutionIf equilibrium constant for the reaction
A2+B2⇔2AB is k, then for the backward reaction AB⇔1/2A2+1/2B2 the equilibrium constant k' is 1/K.View SolutionThe following pictures represents the equilibrium state for three different reactions of the type
A2+X2⇔2AX (X=B,CorD)
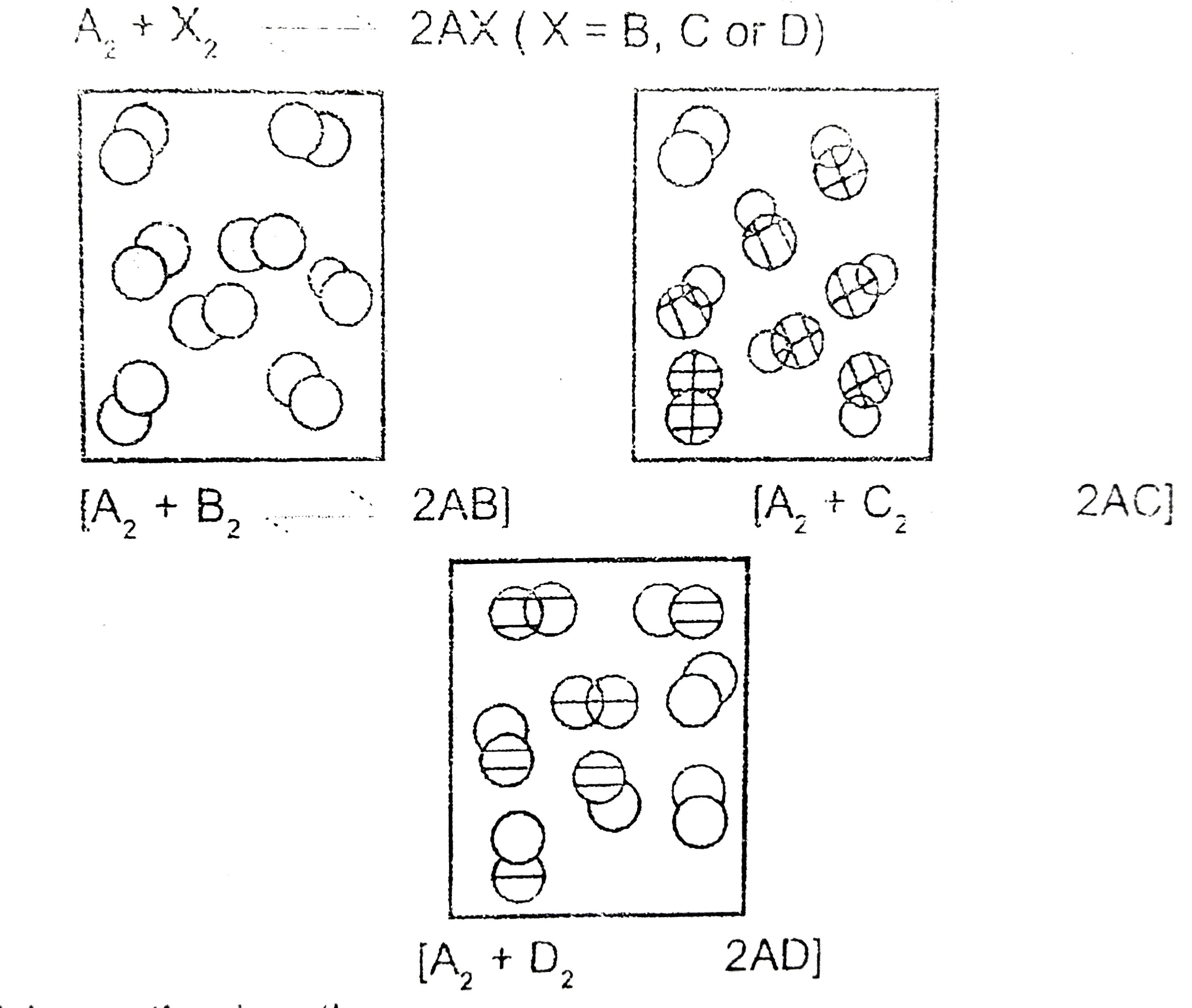
Which reaction has the largest equilibrium constant?View SolutionMechanism of the reaction is:
A2k⇐⇒k'2A
A+B2k2−−→C+B
B+A2k2−−→C+A
What is−d[A2]dtView SolutionConisder the reaction mechanism:
A2keq⇐⇒2A(fast) (where A is the intermediate.)
A+B−−→k1P(slow)
The rate law for the reaction isView Solution
