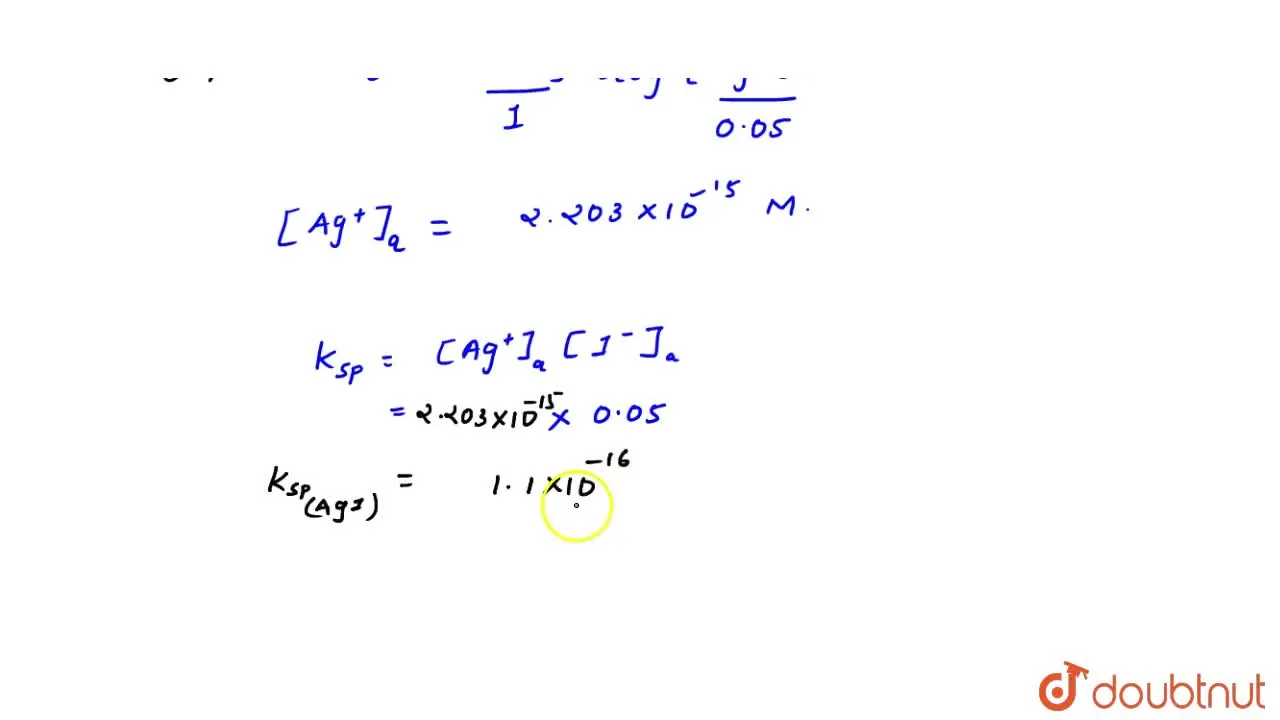The e.m.f of cell Ag∣∣AgI(s),0.05MKI∣∣|0.05MAgNO3|Ag is 0.788V. Calculate solubility product of AgI.
KSP of AgI=[Ag+][I−]=[Ag+][0.05]
For given cell ECell=EOPAg+ERPAg …(1)
=EOPAg/Ag+−0.0591log[Ag+]L.H.S.
+ERPAg+/Ag−0.0591log[Ag+]R.H.S.
ECell=0.0591log[Ag+]R.H.S.[Ag+]L.H.S.
[∵E∘OPAg/Ag+=E∘RPAg+/Ag]
=0.788=log0.05[Ag+]L.H.S.
∴[Ag+]L.H.S.=2.203×10−15
By eq. (1) KSP=[2.203×10−15][0.05]
KSPAgI=1.10×10−16
Related Playlists
- BOOK - P BAHADURCHAPTER - ELECTROCHEMISTRYEXERCISE - (A) ELECTROLYSIS2videos
ELECTROCHEMISTRY
- BOOK - P BAHADURCHAPTER - ELECTROCHEMISTRYEXERCISE - (B) ELECTRODE POTENTIAL AND EMF1videos
ELECTROCHEMISTRY
- BOOK - P BAHADURCHAPTER - DILUTE SOLUTION AND COLLIGATIVE PROPERTIESEXERCISE - Exercise 9 Advanced Numerical12videos
DILUTE SOLUTION AND COLLIGATIVE PROPERTIES
- BOOK - P BAHADURCHAPTER - MOCK TEST PAPEREXERCISE - Exercise92videos
MOCK TEST PAPER
Similar Questions
The emf of the cell,
Ag|AgI(0.05)MKI||(0.05)MAgNO3|Ag
is 0.788 volt. Calculate the solubility product of AgI.View SolutionThe emf of the cell
Ag|AgI|KI(0.05M)∣|AgNO3(0.05M)|Ag is 0.788 V. Calculate the solubility product of AgI.View SolutionThe e.m.f of cell Ag∣∣AgI(s),0.05MKI∣∣|0.05MAgNO3|Ag is 0.788V. Calculate solubility product of AgI.
View SolutionThe emf of the cell Ag|KI(0.05M)||AgNO3(0.05M)|Ag is 0.788V. Calculate the solubility product of AgI.
View SolutionThe emf of the cell Ag|AgI|CI(0.05M)∣|AgNO3(0.05M)|Ag is 0.79 V. Calculate the solubility product of AgI.
View SolutionThe EMF of cell
Ag|AgCl,0.05MKCl||0.05MAgNO3|Ag is 0.788 Volt.
Find the solubility product of AgCl.View SolutionThe EMF of the cell :
Ag|Ag2CrO4(s),K2CrO4(0.1M)||AgNO3(0.1M)|∣Ag is 206.5mV. Calculate the solubility of Ag2CrO4 in 1MNa2CrO4 soluion.View SolutionThe EMF of cell
Ag|AgCl,0.05MKCl||0.05MAgNO3|Ag is 0.788 Volt.
Find the solubility product of AgCl.View SolutionThe e.f.m. of the cell Ag∣∣Ag+(0.1M)∣∣∣∣Ag+(1M)∣∣Ag at 298K is
View SolutionThe EMF of the cell :
Ag|AgCl,0.1MKCl||0.1MAgNO3|Ag is 0.45V.0.1MKClis 85% dissociated and 0.1MAgNO3 is 82% dissociated. Calculate the solubility product of AgCl at 25∘C.View Solution