HOW TO CALCULATE EMF OF CELL?
How to Calculate EMF of a Cell
What is Electromotive Force (EMF)?
The electromotive power (EMF) is the highest potential difference between two electrodes of a galvanic or voltaic cell. This amount is identified with the tendency of an atom to accept (gain) or release (lose) electrons. For instance, the most extreme potential among Zn and Cu of a notable cell has been measured to be 1.100 V.
Zn(s) | Zn2+(1M) || Cu2+(1M) | Cu(s)
In an ideal solution, a concentration of 1 M is characterized as the typical condition, and 1.100 V is the standard electromotive power, Eo, or standard cell potential for the Zn−Cu galvanic cell.
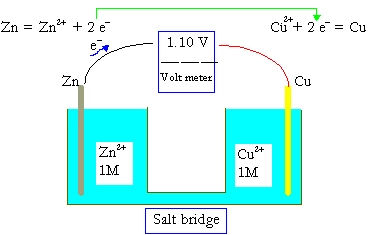
The standard cell potential of a galvanic cell can be assessed from the standard reduction potentials of the two half cells. The reduction potentials are evaluated against the standard hydrogen anode (SHE):
Pt(s) | H2(g,1.0atm) | H+(1.0M)
Its reduction potential or oxidation potential is characterized to be actually zero.
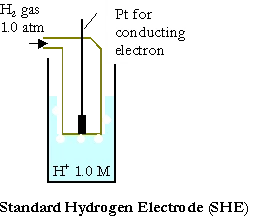
The reduction potentials of all other half-cells calculated in volts regarding the SHE are the difference in potential energy (electrical) for each coulomb of charge.
Unit for energy, J = coulomb volt,
Gibbs free energy (G) is the result potential difference( E) and of charge (q)
G ( in J) = q E (in C V) for electric energy computations.
Standard Cell Potential of Galvanic Cells
A galvanic cell has two half-cells. The galvanic cell convention of writing is to put the (reduction) cathode on the right side, and the (oxidation) anode on the left side.
Pt|H2|H+ || Zn2+|Zn
For instance, the cell comprises the reduction and oxidation reactions:
H2 → 2e− + 2H+ anode (oxidation) reaction
Zn2+ + 2e− → Zn cathode (reduction) reaction
On the off chance that the concentrations of H+ and Zn2+ ions are 1.0 M and the pressure of H2 is 1.0 atm, the voltage difference between the two electrodes would be - 0.763 V(the Zn cathode being the negative terminal). The conditions specified above are known as the standard conditions and the EMF so acquired is the standard reduction potential of the cell.
The above cell representation is in reverse order in comparison with that given in numerous textbooks; however, this orientation indicates the standard reduction potentials directly, because the Zn half cell is a reduction half-cell. The negative voltage suggests that the reverse chemical reaction is spontaneous. This corresponds to the way that Zn metal reacts with an acid to deliver H2 gas.
As another model, the cell represented as Pt|H2|H+ || Cu+|Cu comprises of a reduction reaction and an oxidation reaction.
H2 → 2e− + 2H+ anode reaction
Cu2+ + 2e− → Cu cathode reaction
The standard cell potential is equal to 0.337 V. The positive potential signifies a spontaneous reaction,
Cu2++ H2 → Cu + 2H+
In any case, the potential is so small that the reaction is too slow to be in any way observed.
Related Video:
Equations to Calculate EMF
There are two primary equations for computing EMF. The most essential definition is the quantity of joules of energy (E) every coulomb of charge (Q) selects as it flows through the cell.
ε = E ÷ Q
Here
ε à symbol for electromotive power,
E à the circuit energy
Q à the charge of the circuit.
If the resulting energy and the measure of charge passing through the cell is given, then it is the simplest method to compute EMF; however, you won't have that information often.
Find EMF by the formula:
ε = V + Ir
Here
V à the voltage of the cell
I à the current in the circuit
r à the inside resistance of the cell.
It can also be written and used in the form of Ohm's law (V = IR).
On comparing Ohm's law with EMF equation, it can be written as:
ε = I (R + r)
Here
I à current
R à resistance of the circuit
R à the inner resistance of the cell.
The similarity of two equations (a) & (b) mentioned below
ε = IR + Ir …. (a)
= V + Ir …. (b)
shows that you can compute the EMF in the event that the voltage across the terminals and the current flowing and the interior resistance of the cell are given.
Steps to Calculate EMF
Sample Problem 1: If there is a circuit with a potential difference of 3.2 V, current of 0.6 A flowing with the internal battery resistance at 0.5 ohms. Find the EMF of the cell.
Sol 1: Given: V= 3.2 V
I= 0.6A
r= 0.5 ohms
We know that, ε = V + Ir
Putting the given values in the above formula, we get:
= 3.2 V + 0.6 A × 0.5 Ω
= 3.2 V + 0.3 V = 3.5 V
So the EMF of the circuit is 3.5 V.
The above example shows how to compute the EMF of the cell using standard reduction potentials.
Sample Problem 2: Calculate the emf of a cell (under standard conditions) in which Zinc metal combines with an acid to yield Zinc ions and hydrogen gas?
Sol 2: The first step is to write the half-cell reactions as one-electron reductions R:
If the cell isn't depicted, assign right- and left-hand reactions randomly
R: H + + e- → ½ H2 (g) Eo=0 V (as per definition)
L: ½ Zn2+ + e = Zn (s) Eo = - 0.76V
Since the EMF is an intensive property; therefore, it does not depend upon the amount of material is reacting. If we divide the reduction equation by some number, as done in the second equation above, the emf does not get change.
Cell emf is Eo right – Eo left
Thus, (R – L) à H+ (aq) + ½ Zn (s) = ½ H2 (g) + ½ Zn2+ (aq)
EMF of cell = + 0.76V.
Sample Problem 3:: Calculate EMF of the cell for the reaction between Zn and Fe3+ / Fe2+
Sol 3: As the steps followed in the previous problem,
We first write right- and left-hand reactions randomly
R: Fe3+ (aqueous) + e- (aqueous) = Fe2+ (aqueous)…..Eo= + 0.77V
L: ½ Zn2+ (aq) + e - (aq) = ½ Zn (s)…. .Eo = - 0.76V
Since the EMF is an intensive property; therefore, it does not depend upon the amount of material is reacting. If we divide the reduction equation by some number, as done in the second equation above, the emf does not get change.
Cell emf is Eo right – Eo left
- (R – L): Fe 3+ (aq) + ½ Zn (s) = Fe2+ (aq) + ½ Zn2+ (aq)....
EMF of cell = +0.77 – (- 0.76) = + 1.53V
Important Chapters:


Similar Questions
Knowledge Check
- Question 1 - Select One
The EMF of a cell is
Asum of two oxidation potentialsBsum of two potentialsCdifference of two electrode potentialsDNone of the above - Question 2 - Select One
The EMF of a Daniel cell
A0 voltB5 voltsC1.1 voltsD3 volts - Question 3 - Select One or More
Daniel cell, the EMF of the cell can b e increased b y
Aincreasing the concentration af Zn+ ionsBdecreasing the concentration of Cu2+Cincreasing the concentration of Cu2+Ddecreasing the concentration of Zn2+ ions
Numericals of EMF of Cell
View SolutionCell & EMF Of Cell |Combination Of Cells|Series Combination Of Cell|Parallel Combination Of Cell
View SolutionComparision Of Emf Of Two Cells
View SolutionThe cell EMF is independent of the concentration of the species of the cell in
View SolutionThe two half cell reactions of an electrochemical cell is given as
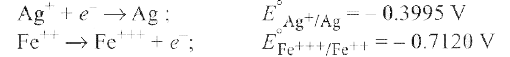
the value of cell EMF will beView Solution
