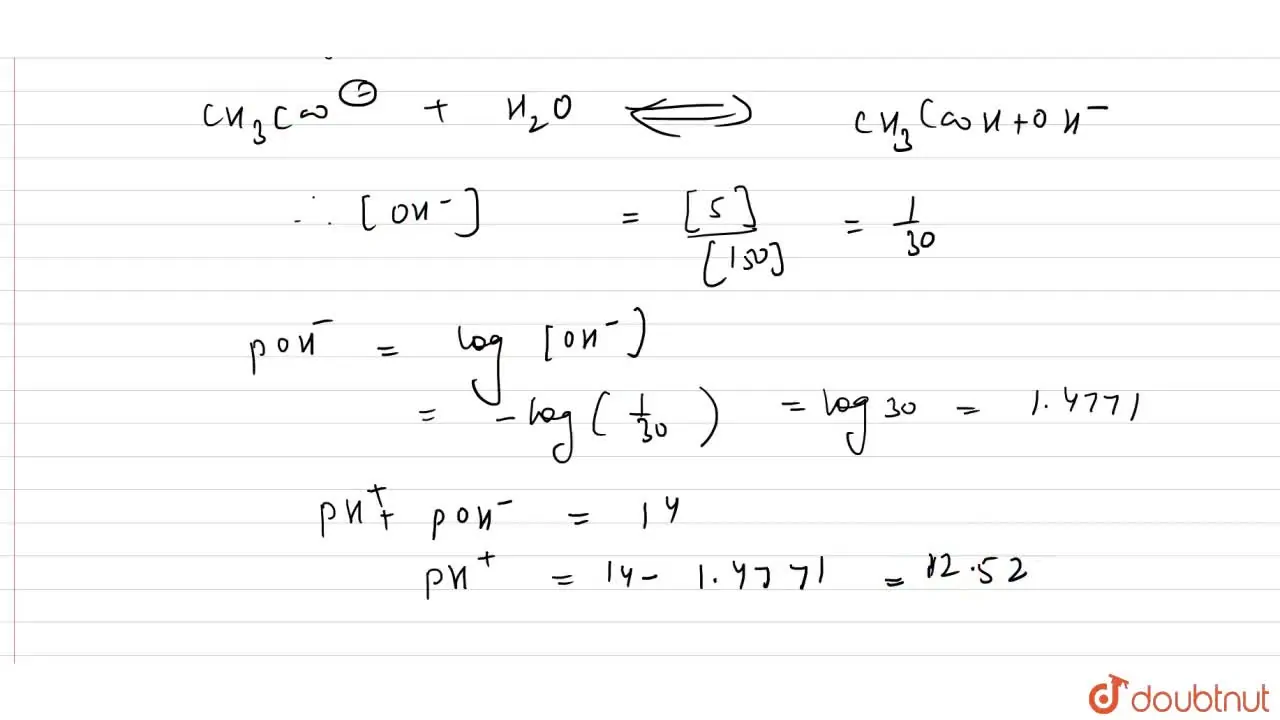Calculate the pH of each of the following solution
(i) 100 ml of 0.1 M CH3COOH mixed with 100 ml of 0.1 M NaOH.
(ii) 100 ml of 0.1 M CH3COOH mixed with 50 ml of 0.1 m NaOH
(iii) 50mlof0.1MCH3COOH mixed with 100 ml of 0.1 M NaOH.
Ka(CH3COOH)=1.8×10−5
(a) CH3COOH1 mole+NaOH1 mole→CH3COONa1 mole+H2O1 mole
m. moles of Ch3COOH=0.1×100=10
m moles of NaOH=100×0.1=10
Therefore, m. moles of CH3COONa is 10
Now in the solution only salt CH3COONa is present, therefore, pH of solution can be calculated by the hydrolysis of CH3COONa
CH3COONa is a salt of weak acid with strong base
pH=7+12pKa+12logC
=7+12×4.75+12log(10200) (pKa=−log1.8×10−5)
=8.72 pKa=4.75
(b) CH3COOH+NaOH→CH3COONa+H2O
Initial m moles10500m moles after reaction10−5055
Since in the solution, mixture of CH3COOHandCH3COONa is present therefore, solution is an acidic buffer and pH can be calculated as
pH=pKa+log[salt][acid]pH=4.75+log⎛⎝52005200⎞⎠pH=4.75
(c ) CH3COOH+NaOH→CH3COONa+H2O
Initial m moles51000m moles after reaction0(10−5)55
Now in the solution strong base NaOH and salt of weak aid with strong base is present We can assume that OH− ions concentration from the hydrolysis of salt is negligible because hydrlysis of CH3COONa is suppressed by the presence of strong base NaOH.
CH3COO−(from salt)+H2O⇔CH3COOH+OH−
∴[OH−]=[5][150]=(130)
pOH=log[OH−]=−log(130)=log30=1.4771
pH+pOH=14
pH=14−1.4771=12.52
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - EQUILIBRIUMEXERCISE - TRY YOURSELF52videos
EQUILIBRIUM
- BOOK - AAKASH INSTITUTECHAPTER - EQUILIBRIUMEXERCISE - Assignment (SECTION-A) (SUBJECTIVE TYPE QUESTIONS(ONE OPTION IS CORRECT)45videos
EQUILIBRIUM
- BOOK - AAKASH INSTITUTECHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - ASSIGNMENT (SECTION-D) (Assertion - Reason Type Questions)5videos
ENVIRONMENTAL CHEMISTRY
- BOOK - AAKASH INSTITUTECHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSEXERCISE - Assignment (Section-D) Assertion-Reason Type Question15videos
GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS
Similar Questions
Calculate the amount of heat released when:
(i) 100 mL of 0.2 M HCl solution is mixed with 50 mL of 0.2 M KOH.
(ii) 200 mL of 0.1 M H2SO4 is mixed with 200 mL of 0.2 M KOH solution.View Solution100ml of 0.1MCH3COOH are mixed with 100ml of 0.1MNaOH, the pH of the resulting solution would be
View SolutionWhat is the pH of the solution when 100mL of 0.1MHCl is mixed with 100mL of 0.1MCH3COOH.
View SolutionIn which of the following mixed aqueous solutions pH = pka at equilibrium?
(1) 100mLof0.1MCH3COOH+100mLof0.1MCH3COONa
(2)100mLof0.1MCH3COOH+50mLof0.1MNaOH
(3) 100mLof0.1MCH3COOH+100mLof0.1MNaOH
(4)100mLof0.1MCH3COOH+100mLof0,1MNH3View SolutionCalculate the pH of resulting solution, when 50 mL of 0.20MHCI is mixed with 50 mL of 0.20MCH3COOH.
View SolutionCalculate the molarityes and normalities of the solution obtained on mixing
(i) 100 mL of 0.2 M H2SO4 with 50 mL of 0.1 M HCl
(ii) 100 mL of 0.2 N H2SO4 with 50 mL of 0.1 N HCl
(iii) 100 mL of 0.1 M H2SO4 with 50 mL of 0.1 M NaOH
(iv) 50 mL of 0.1 N H2SO4 with 100 mL of 0.1 N NaOH.View SolutionThe pH of a solution obtained by mixing 100 mL of 0.2 M CH3COOH with 100 mL of 0.2 M NaOH would be :(pKa for CH3COOH=4.74)
View Solution10ml of 0.1MCH3COOH is mixed with 990ml of 0.01MNaCl solution. What is the change in pH of CH3COOH solution
View SolutionCalculate pH of the following mictures , Given that Ka=1.8×10−5andKb=1.8×10−5
(a) 50 mL of 0.05 NaOH + 50 ml of 0.10 M CH3COOH
(b) 50 ml of 0.10 NaOH + 50 ml of 0.10 M CH3COOHView SolutionWhich of the following will have nearly equal [H+] concentration ?
(i)100 ml 0.1 M HCl mixed with 50 ml of water
(ii) 50 ml of 0.1 M H2SO4 mixed with 50 ml of water
(iii) 50 ml of 0.1 M H2SO4 mixed with 100 ml of water
(iv) 50 ml of 0.1 M HCl mixed with 50 ml of waterView Solution