AX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣
∣
∣
∣
∣
∣
∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣
∣
∣
∣
∣
∣
∣∣
A salt MY crystallizes in the CsCl structure. The anions at the corners touch each other and cation is in the centre. The radius ratio (r⊕/rΘ) for this structure is
0.225
0.414
0.732
1.0
The correct Answer is:C
To solve the problem, we need to find the radius ratio r+r− for the cesium chloride (CsCl) structure, where r+ is the radius of the cation and r− is the radius of the anion.
1. Understanding the Structure:
- CsCl has a body-centered cubic (BCC) structure.
- The anions are located at the corners of the cube, and the cation is located at the center.
2. Finding the Distance Between Anions:
- The distance between two opposite corner anions (let's say A and B) can be calculated using the body diagonal of the cube.
- The body diagonal d of a cube with edge length a is given by:
d=√3a
3. Relation of Distances:
- In the CsCl structure, the distance between the centers of the anions (corner anions) is equal to the distance from the center of the cation to the center of a corner anion plus the distance from the center of the cation to the center of the opposite corner anion.
- This can be expressed as:
d=2r−+2r+
- Therefore, we can write:
√3a=2r−+2r+
4. Finding the Edge Length:
- For the CsCl structure, the edge length a can be expressed in terms of the radii:
a=2r−
- Substituting this into the equation for d:
√3(2r−)=2r−+2r+
5. Simplifying the Equation:
- Dividing the entire equation by 2:
√3r−=r−+r+
- Rearranging gives:
r+=√3r−−r−=(√3−1)r−
6. Finding the Radius Ratio:
- The radius ratio r+r− can now be calculated:
r+r−=(√3−1)r−r−=√3−1
- Evaluating √3:
√3≈1.732
- Thus:
r+r−≈1.732−1=0.732
Conclusion:
The radius ratio r+r− for the CsCl structure is approximately 0.732.
- CsCl has a body-centered cubic (BCC) structure.
- The anions are located at the corners of the cube, and the cation is located at the center.
- The distance between two opposite corner anions (let's say A and B) can be calculated using the body diagonal of the cube.
- The body diagonal d of a cube with edge length a is given by:
d=√3a
- In the CsCl structure, the distance between the centers of the anions (corner anions) is equal to the distance from the center of the cation to the center of a corner anion plus the distance from the center of the cation to the center of the opposite corner anion.
- This can be expressed as:
d=2r−+2r+
- Therefore, we can write:
√3a=2r−+2r+
- For the CsCl structure, the edge length a can be expressed in terms of the radii:
a=2r−
- Substituting this into the equation for d:
√3(2r−)=2r−+2r+
- Dividing the entire equation by 2:
√3r−=r−+r+
- Rearranging gives:
r+=√3r−−r−=(√3−1)r−
- The radius ratio r+r− can now be calculated:
r+r−=(√3−1)r−r−=√3−1
- Evaluating √3:
√3≈1.732
- Thus:
r+r−≈1.732−1=0.732
The radius ratio r+r− for the CsCl structure is approximately 0.732.
Topper's Solved these Questions
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (Multiple Correct)
Explore 39 Videos
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (Single Correct)
Explore 72 Videos
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Solved Examples
Explore 13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBook:CENGAGE CHEMISTRY ENGLISHChapter:REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSExercise:SUBJECTIVE TYPE
Explore 4 Videos
- SOLUTIONSBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLUTIONSExercise:Ex 2.3 (Objective)
Explore 9 Videos
Similar Questions
AX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
Ionic radii of X⊕ and YΘ, respectively, are
View SolutionAX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
Which of the following structure is, respectively, by Ax?
(a)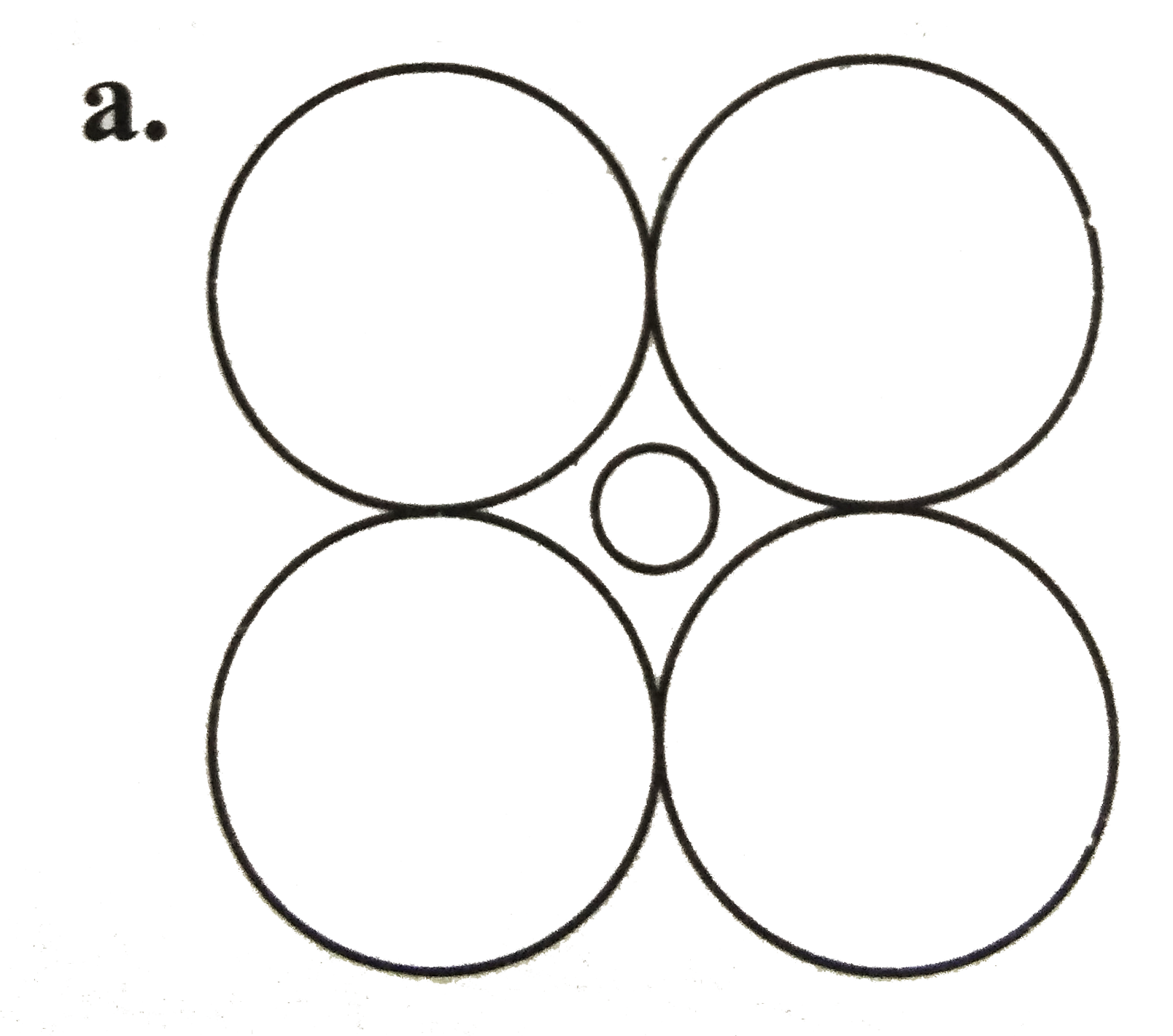
(b)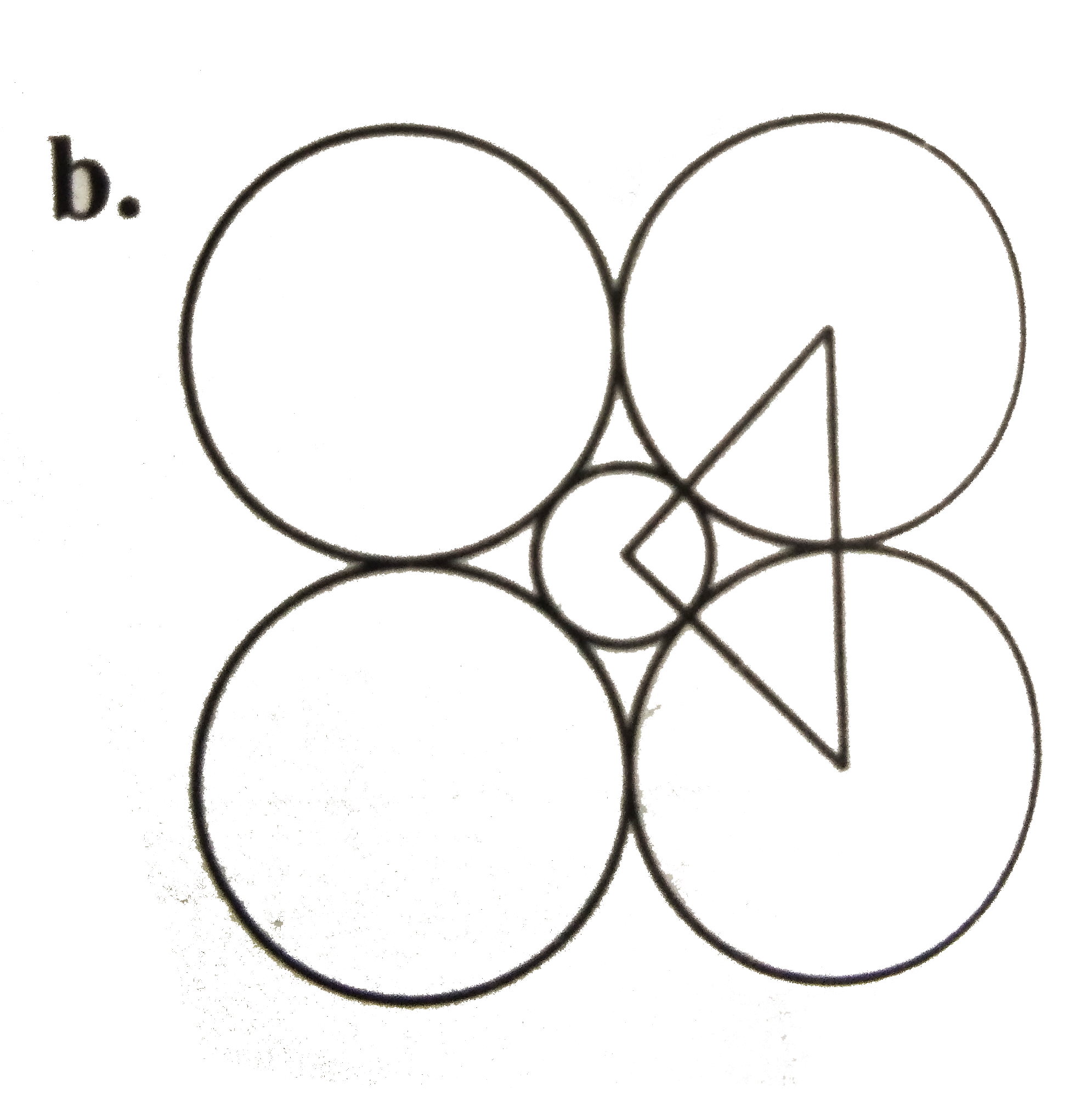
(c)
(d)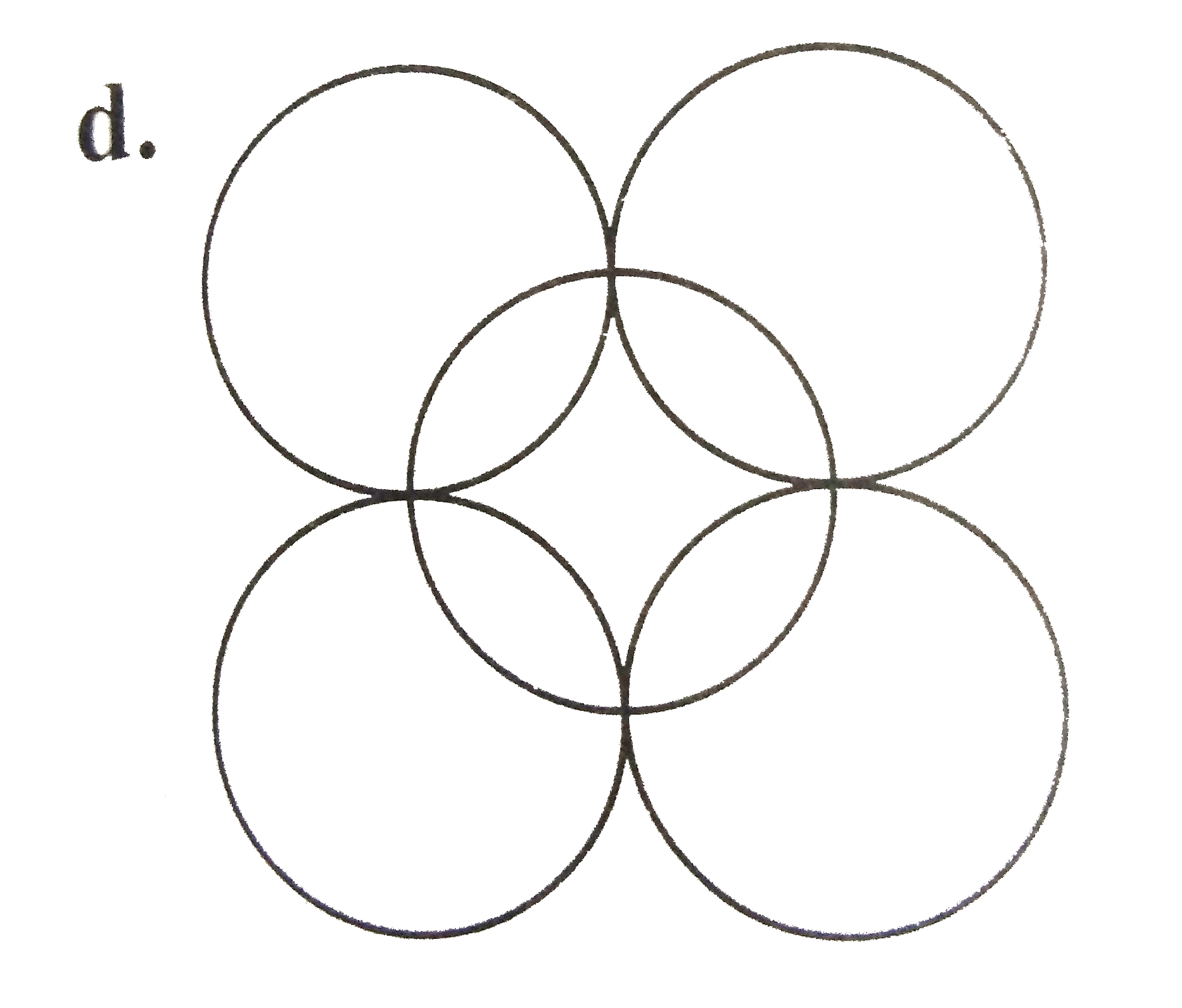
View SolutionAX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
The structure given below is of

(a)AX
(b)AY,BX
(c)AY,BX,BY
(d)AY,BX,BYandKCI
View SolutionAX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
Ionic radii of A⊕ and B⊕, respectively, are
a.0.35 and 0.68Å
b.0.68 and 0.35Å
c.1.20 and 0.80Å
d.0.80 and 1.20Å
View SolutionIn the fluorite structure if the radius ratio is (√32−1) how many ions does each cation touch?
View SolutionAssertion:- Antifluorite structure is 4:8 (cation:anion) type coordination crystal.
Reason:- Ratio of no. of cation and anions in CaF2 crystal is 1:2
View SolutionSuggest the probable structures of the unit cells of the following each compound with the help of given data
∣∣ ∣ ∣ ∣ ∣ ∣∣Cationic radiusAnionic radius(a)RbBe1.04Å1.95Å(b)MeTe0.65Å2.21Å(c)MgO0.65Å1.40Å(d)BaO1.35Å1.40Å∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionSalt AB has a zinc blend structure. The radius of A2+ and B2− ion are 0.7Åand1.8Å respectively. The edge length of AB unit cell is:
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
The student performs another trial in which the ball is launched at speed 5.0m/s. Its range is approximately:
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View Solution

