In the figure, from top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid.
[ Use $π = \frac{22}{7} and \sqrt{5} = 2.236 .$ ]

Video Solution

Text Solution

Verified by Experts

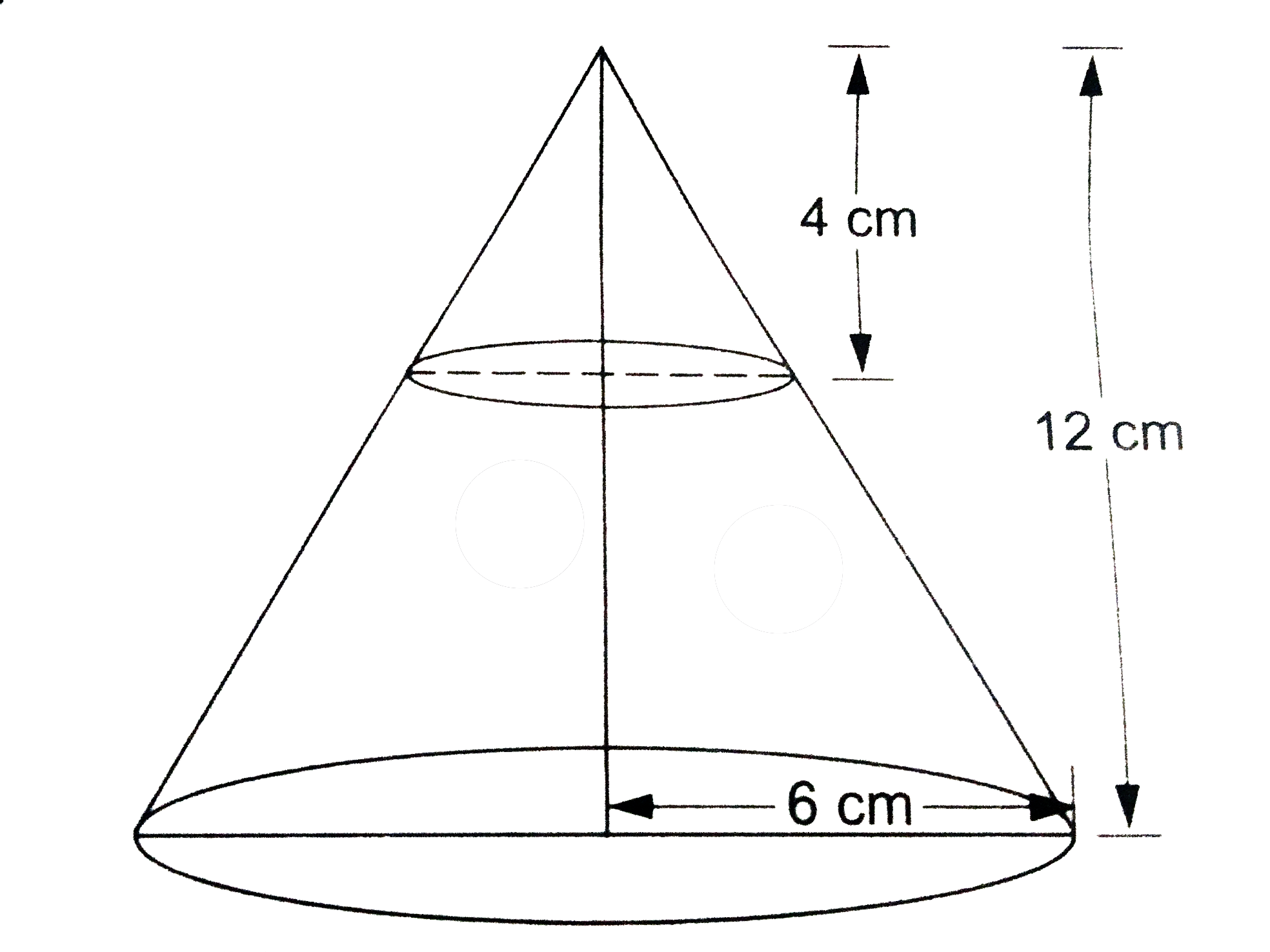
Clearly, the remaining solid is the frustum CDBA of cone OPD. Radius of lower end of the frustum, R = CD = 6 cm.
Height of the frustum,
h = AC = OC - OA
$= (12 - 4) c m = 8 c m$ .
Let the radius of upper face be r cm.

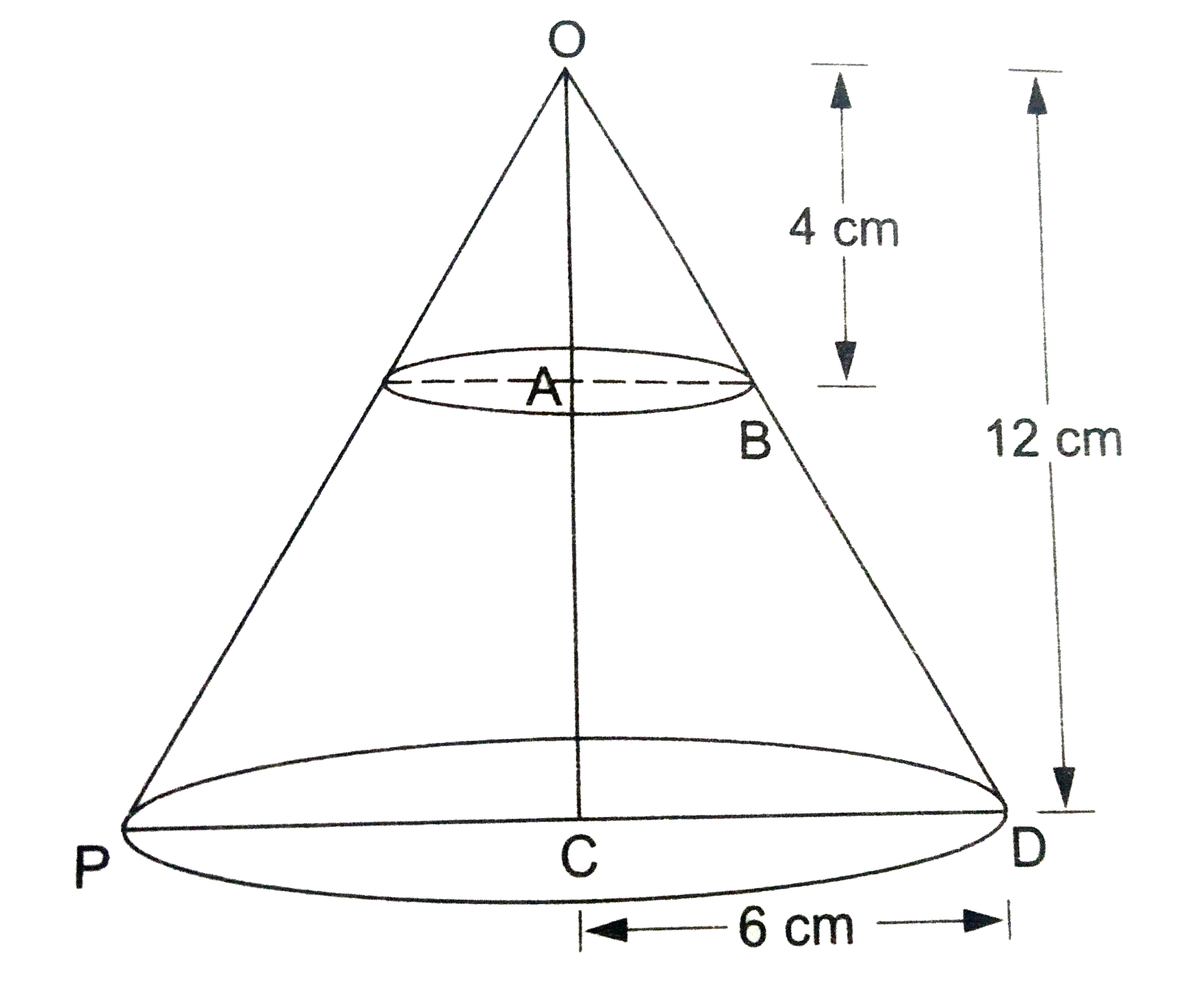
Now, $Δ O A B ~ Δ O C D$ .
$So, \frac{O A}{O C} = \frac{A B}{C D} \Rightarrow \frac{4}{12} = \frac{r}{6}$
$\Rightarrow r = (\frac{4}{12} \times 6) c m = 2 c m$ .
Slant height of the frustum,
$l = \sqrt{h^{2} + {(R - r)}^{2}} = \sqrt{8^{2} + {(6 - 2)}^{2}} = \sqrt{80} x m = 4 \sqrt{5} c m$ .
Total surface area of the frustum
= area of base + area of top + curved surface area
$= π R^{2} π r^{2} + π l (R + r) = π [R^{2} + r^{2} + l (R + r)]$
$\frac{22}{7} \times [6^{2} + π r^{2} + π l (R + r) = π [R^{2} + r^{2} + l (R + r)]$
$= [\frac{22}{7} \times (36 + 4 + 71.552)] c m^{2} = (\frac{22}{7} \times 11.552) c m^{2}$
$= (22 \times 15.936) c m^{2} = 350.592 c m^{2}$ .

Updated on:21/07/2023

|

Class 10 MATHS SURFACE AREAS AND VOLUMES

Similar Questions

Knowledge Check

From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
A $240 π$ cu. cm
B5280 cu. cm
C $620 π$ cu. cm
D $360 π$ cu. cm

Recommended Questions

Home
Ask Doubt
Profile