A solid sphere of radius R has total charge 2Q and volume charge density p=kr where r is distance from centre. Now charges Q and −Q are placed diametrically opposite at distance 2a where a is distance form centre of sphere such that net force on charge Q is zero then relation between a and R is
a=8−1/4R
a = (3R)/(2^¼)
a=2−1/4R
a=R/√3
The correct Answer is:A
Step by step video & text solution for A solid sphere of radius R has total charge 2Q and volume charge density p=kr where r is distance from centre. Now charges Q and -Q are placed diametrically opposite at distance 2a where a is distance form centre of sphere such that net force on charge Q is zero then relation between a and R is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid sphere of radius R is charged with volume charge density p=Krn , where K and n are constants and r is the distance from its centre. If electric field inside the sphere at distance r is proportional to r4 ,then find the value of n.
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View Solution
Knowledge Check
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2Let a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
Aa=2−1/4RBa=R√3Ca=8−1/4RDa=3R21/4A sphere of radius R, is charged uniformly with total charge Q. Then correct statement for electric field is (r = distance from centre): -
AKQrR3, where r<RBKQr2, where r≥RCit is zero, at all pointsD(A) and (B) both
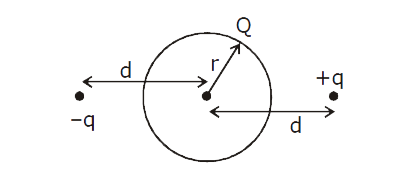
A solid conducting sphere of radius r is having a charge Q and point charges +q and -q are kept at distance d from the centre of sphere as shown in the figure. The electric potential at the centre of solid sphere
(assume potential to be 0 at infinity)
View SolutionA sphere of radius R_(0 carries a volume charge density proportional to the distance (x) from the origin, rho=alpha x where alpha is a positive constant.The total charge in the sphere of radius R_(0) is
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View Solution
