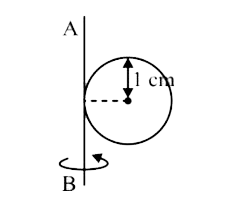
A metal coinn of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass as shown in the figure. The system is initially at rest. The constant torque, hat will make the system rotate about AB at 25 rotations per second in 5s. Is close to

4.0×10−6Nm
1.6×10−5Nm
7.9×10−6Nm
2.0×10−5Nm
The correct Answer is:D
Step by step video & text solution for A metal coinn of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass as shown in the figure. The system is initially at rest. The constant torque, hat will make the system rotate about AB at 25 rotations per second in 5s. Is close to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A metal coin of mass 5 g and radius 1 cm is fixed to a think stick AB of negligible mass as shown in the figure. The system is initially at rest. The constant torque, that will make the system rotate about AB at 25 rotations per second in 5 s, is close to:
View Solution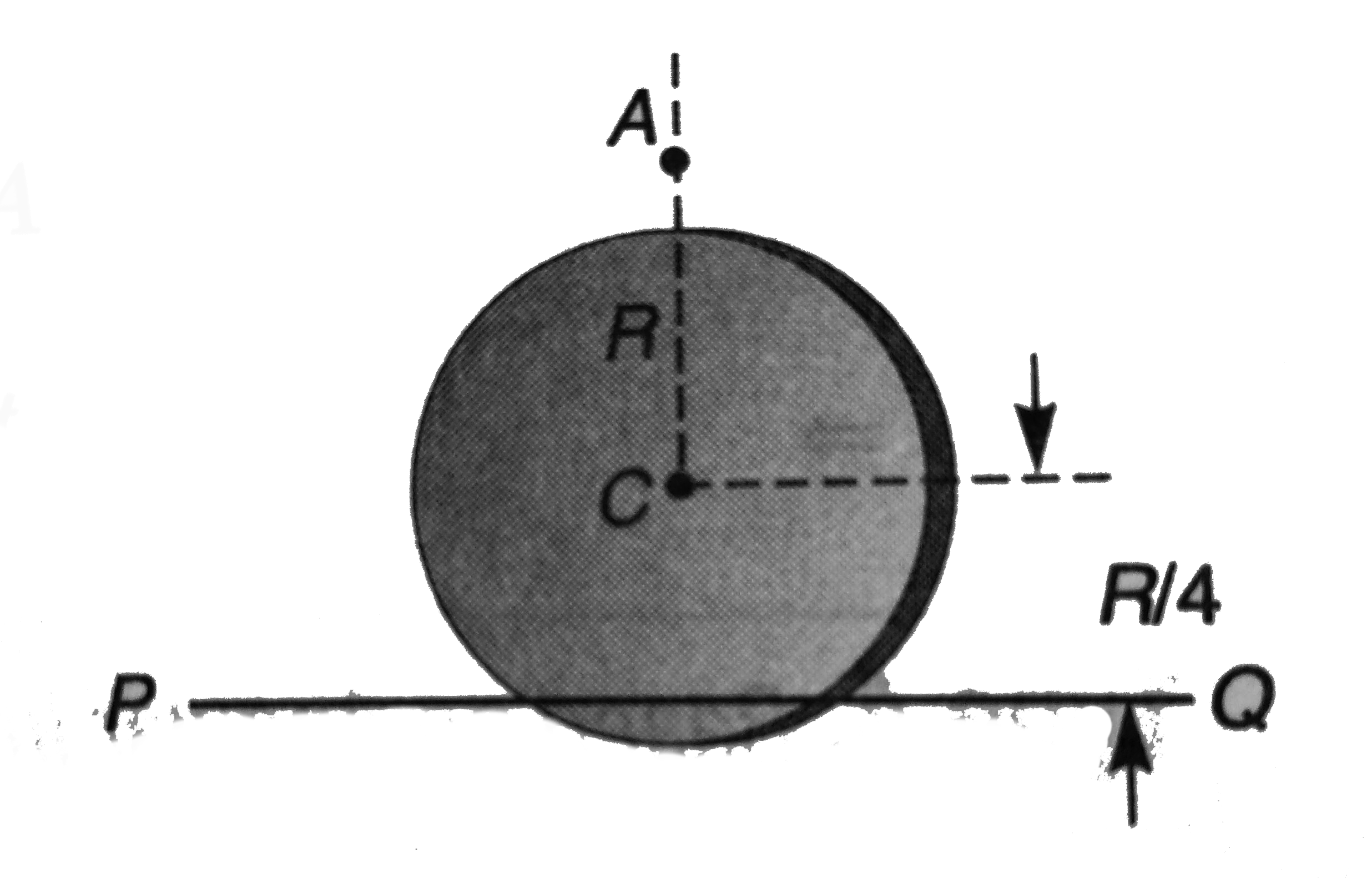
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View Solution
Knowledge Check
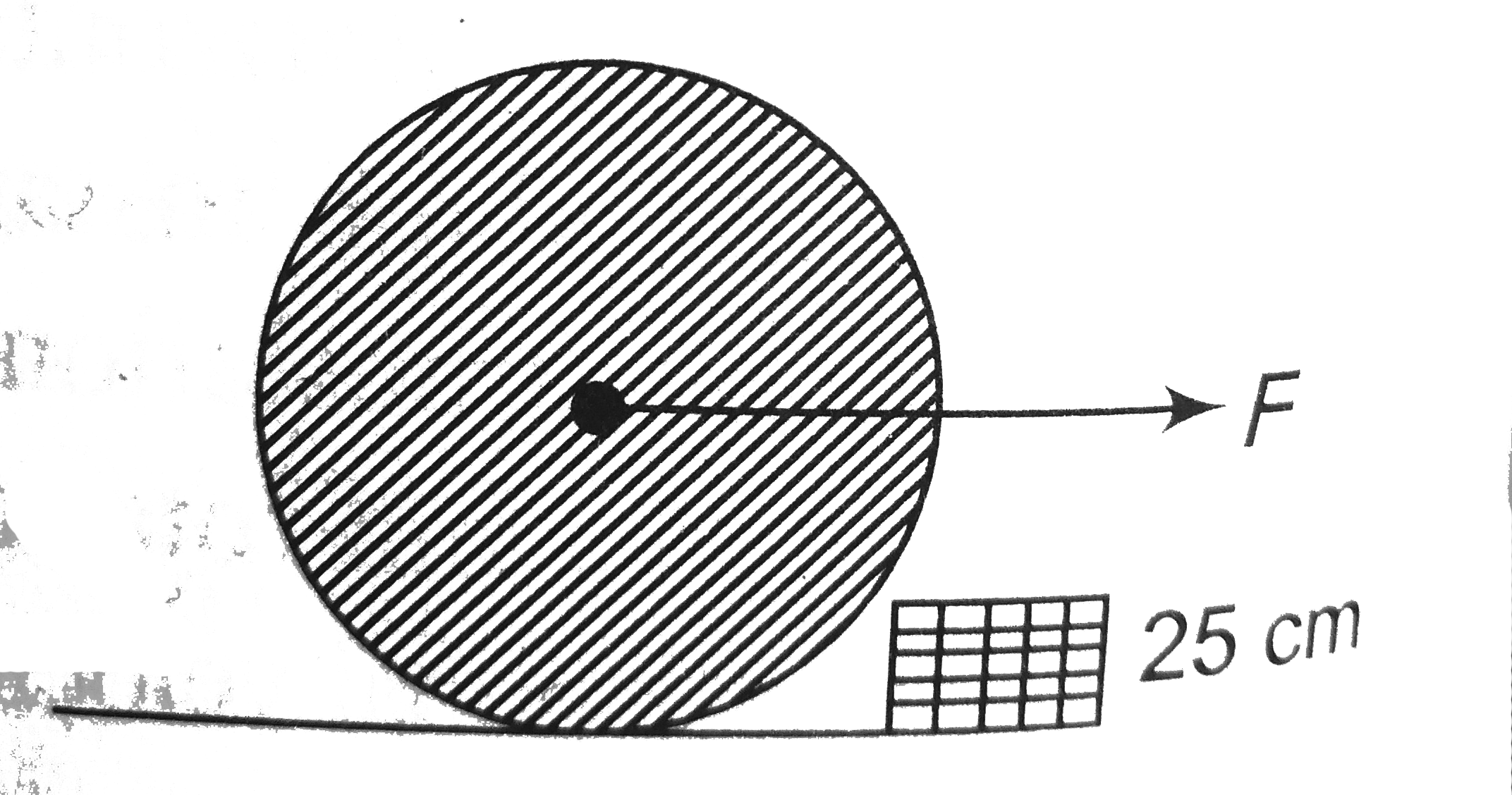
A vertical disc of mass 5kg and radius 50cm rests against a steo of height 25cm as shown in figure. What minimum horizontal force applied perpendicular to the axle will make the disc to climb the step ? Take g=10m/s2.
 .A50 NB50√3NC25NDnone of these
.A50 NB50√3NC25NDnone of theseA mass m is attached to a rigid rod of negligible mass as shown in figure. The system is pivoted at point O and rotates about the indicated z-axis with angular velocity →ω, maintaining a fixed angle θ with the axis.
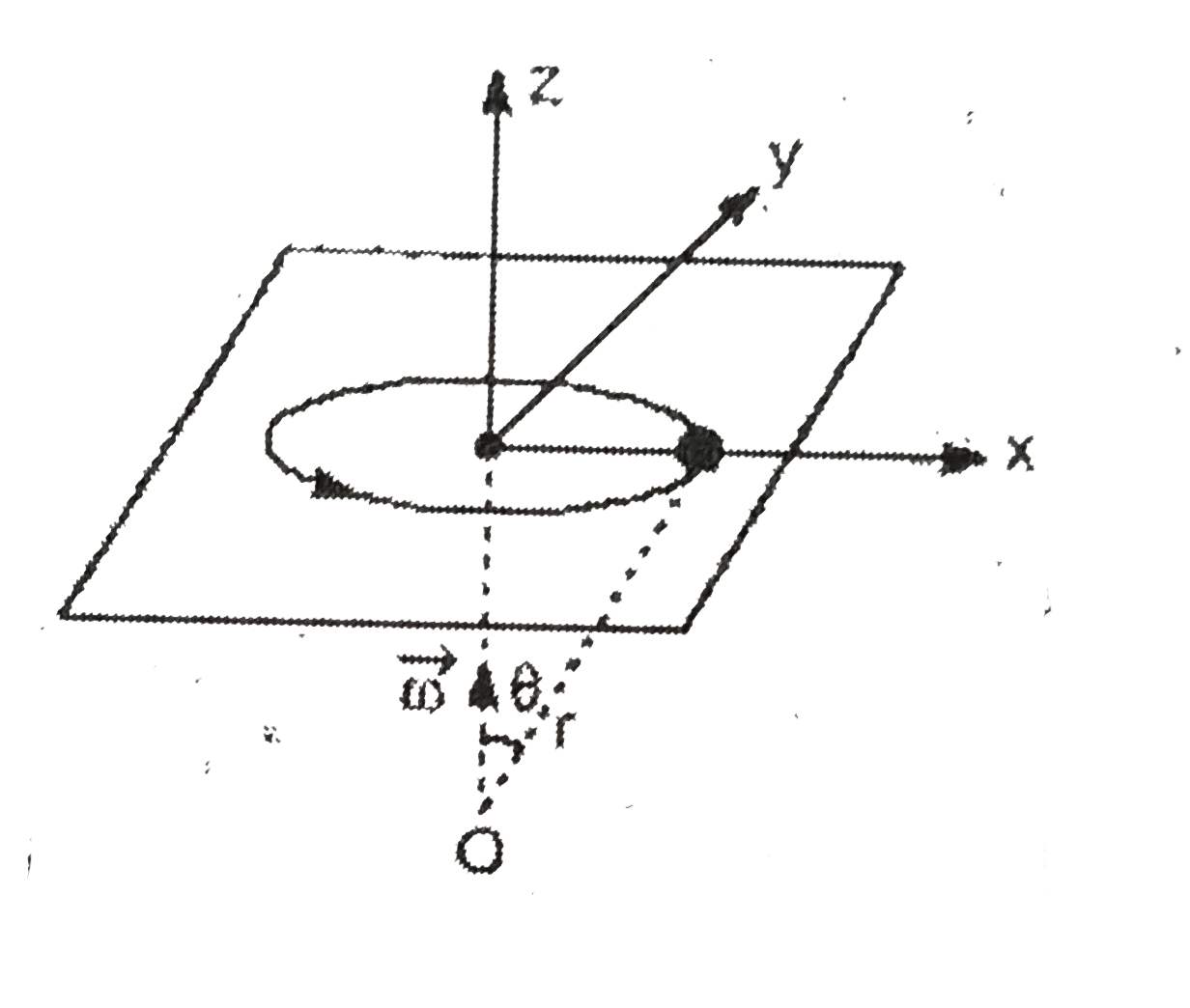 AAngular momentum →L of mass m about pivot is parallel to vector →ωBAngular momentum →L of mass m about pivot is never parallel to →ωC→L0=−mr2ωsinθcosθˆi+mr2ωsin2θˆkDAngular momentum of particle about P is parallel
AAngular momentum →L of mass m about pivot is parallel to vector →ωBAngular momentum →L of mass m about pivot is never parallel to →ωC→L0=−mr2ωsinθcosθˆi+mr2ωsin2θˆkDAngular momentum of particle about P is parallelA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
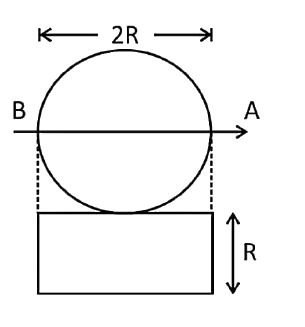
A disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
View SolutionA midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.

View SolutionThree identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be

View SolutionTwo discs A and B each of mass 2kg and radius 0.5m are rigidly fixed to the end of a thin shaft S, which is supported in horizontal position with the help of two smooth bearings at points P1 and P2. Two blocks of masses 2kg and 1kg are connected to the light cords wrapped around the discs as shown in the figure. There is no slipping between the cord and the discs. If the system is released from rest from the position shown, the mark released from rest from the position shown,

View SolutionA whel of mass 2kg an radius 10 cm is rotating about its axis at an angular velocity of 2πrad/s the force that must be applied tangentially to the wheel to stop it in 5 revolutions is
View Solution
