A diet of sick person contains at least 48 units of vitamin A and 64 uints of vitamin B. Two foods F1andF2 are available . Food F1 costs Rs. 6 per unit and food F2 costs Rs. 10 per unit. One unit of food F1 contains 6 units of vitamin A and 7 units of vitamin B. One unit of of food F2 contain 8 units of vitamin A and 12 units of vitamin B. Formulate the LPP, for the minimum cost for the diet that consists of mixture of these two foods and also meeting the minimal nutrition requirements
Let x units of food F1 and y units of food F2 be included in the diet of the sick person.
Then their total cost is z=₹(6x+10y)
This is the objective function which is to be minimized.
The constraints are as per the following table :

From this table, the constraints are
6x+8y≥48,7x+12y≥64
Also, the number of units of foods F1andF2 cannot be negative
∴x≥0,y≥0
∴ the mathematical formulation of given LPP is
Minimize z=6x+10y, subject to
6x+8y≥48,7x+12y≥64,x≥0,y≥0
First we draw the lines AB and CD whose equations are 6x+8y=48and7x+12y=64 respectively.

The feasible region is shaded in the figure.
The vertices of the feasible region are C(647,0), P and B (0,6).
P is the point of intersection of the lines
6x+8y=48 ... (1)
and 7x+12y=64 ...(2)
Multipyting equation (1) by 3 and equation (2) by 2, we get,
18x+24y=144
14x+24y=128
On subtracting, we get,
4x=16
∴x=4
∴ from (1),6(4)+8y=48
∴8y=24
∴y=3
∴P=(4,3)
The values of the objective function z=6x+10y at these vertices are
z(C)=6(647)+10(0)=3847=54.85
z(P)=6(4)+10(3)=24+30=54
z(B)=6(0)+10(6)=60.
∴ the minimum value of z is 54 at the point (4, 3 ).
Hence, 4 units of food F1 and 3 units of food F2 should be included in the diet of the sick person to meet the minimal nutritional requirements, in order to have the minimum cost of ₹ 54.
Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR PROGRAMMING EXERCISE - EXAMPLES FOR PRACTICE
8 Videos
- LINEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEEXERCISE - Multiple choice question
9 Videos
- MATHEMATICAL LOGICBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MATHEMATICAL LOGICEXERCISE - MULTIPLE CHOICE QUESTIONS 2 MARKS EACH
10 Videos
Similar Questions
A diet of a sick person must contains at least 48 units of vitamin A and 64 units of vitamin B. Two foods F1andF2 are available. Food F1 costs Rs. 6 per unit and Food F2 costs Rs. 10 per unit. One unit of food F1 contains 6 units of vitamin A and 7 units of vitamin B. One unit of food F2 contains 8 units of vitamin A and 12 units of vitamin B. Find the minimum cost for the diet that consists of mixture of these two foods and also meeting the minimum nutritional requirements.
View SolutionA diet is to contain at least 80 units of Vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs. 4 per unit and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 units of Vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of Vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
View Solution
Knowledge Check
Structural unit of vitamin-A is
A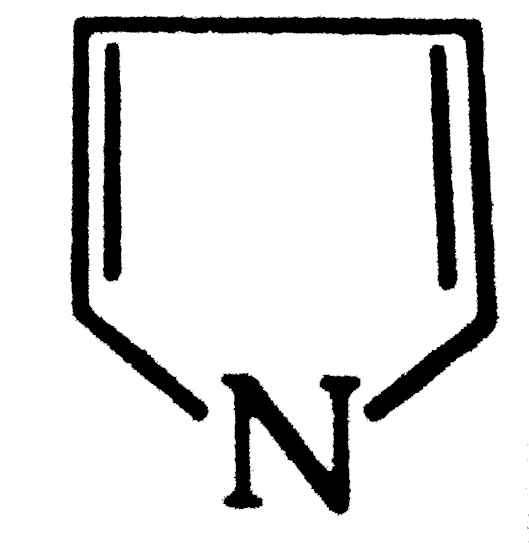 B
B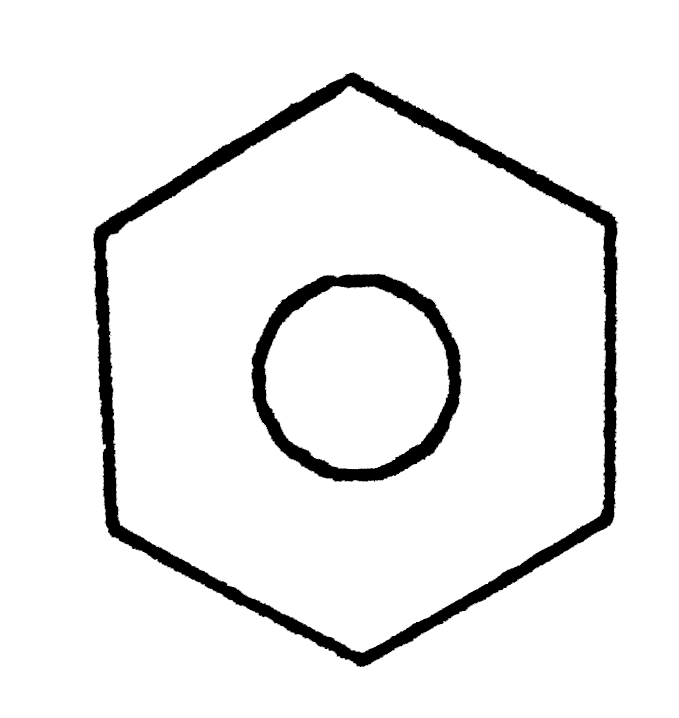 C
C D
D
Diet of a sick person must contains at least 4000 units of vitamins, 50 units of minerals and 2500 calories. Two foods F1andF2 cost Rs. 50 and Rs. 75 per unit respectively. Each unit of food F1 contains 200 units of vitamins, 2 units of minerals and 40 calories,F_(2) contains 100 units of vitamins, 3 units of minerals and 35 calories. Formulate the above problem as LPP to fulfil sick person's requirements at minimum cos.
AMaximized z=50x=75y subject to 200x+100y≥4000,2x+3y≥50,40x+35y≤2500,x≥0,y≥0BMaximized z=50x=75y subject to 200x+100y≤4000,2x+3y≥50,40x+35y≥2500,x≥0,y≥0CMaximized z=50x=75y subject to 200x+100y≥4000,2x+3y≤50,40x+35y≥2500,x≥0,y≥0DMaximized z=50x=75y subject to 200x+100y≥4000,2x+3y≥50,40x+35y≥2500,x≥0,y≥0A diet of a stic person must contain atleast 4000 unit of vitamins, 50 unit of proteins and 1400 calories. Two foods A and B are available at cos of Rs. 4 and Rs. 3 per unit respectively. If one unit of A contains 200 unit of vitamis, 1 unit of protein and 40 calories, while one unit of food B contains 100 unit of vitamins, 2 unit of protein and 40 calories. Formulate the problem, so that the diet be cheapest.
A200x+100y≥400,x+2y≥50
40x+40y≥1400,x≥0andy≥0
O.Fz=4x+3yB400x+200y≥100,x+2y≥50
40x+40y≥1400,x≥0andy≥0
O.Fz=4x+3yC100x+200y≥4000,x+2y≥50,
40x+40y≥1400,x≥0andy≥0
O.Fz=4x+3yDNone of the above
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2, are available. Food F1costs Rs 4 per unit food and F, costs Rs 6 per unit. One unit of food F1, contains 3 units of vitamin A and 4 units of minerals.One unit of foodF2,contains 6 units of vitamin A and 3 units of minerals.Formulate a LPP. find the minimum cost of diet which matches the minimal requirement
View SolutionA diet is to contain at leat 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 cost Rs. 4 per unit and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 uinits of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
View SolutionA diet is to contain at least 4000 units of carbohydrates, 500 units of fat and 300 units of protein. Two foods F1 and F2 are available. Food F1 costs 2 Rs. per unit and food F2 costs 4 Rs. per unit. A unit of food F1 contains 10 units of carbohydrates, 20 units of fat and 15 units of protein. A unit of food F2 contains 25 units of carbohydrates, 10 units of fat and 20 units of protein. Find the minimum cost for a diet that consists of a mixture of these two foods and also meets the minimum requirements.
View SolutionA man wishes to mix two types of food X and Y in such a way that the vitamins contents of the mixture contain at least B units of vitamin A and 11 units of vitamin B. Food X costs Rs. 50 per kg and food Y costs Rs. 60 per kg. Fod Xcontains 2 units per kg of vitamin A and 5 kg per unit of vitamin B while food Y contains 5 units per kg of vitamin A and 2 units per kg of vitamin B. Determine the minimum cost of the mixture.
View SolutionA woman wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food I costs Rs.60/kg and food of vitamin B. Food II cost Rs. 80/kg. Food I contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food II contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Find the minimum cost of the mixture.
View Solution
