If the c.d.f (cumulative distribution function) is given by F(x)=x−2510, then P(27≤x≤33)= . . .
35
310
15
110
The correct Answer is:A
We have,
c.d.f. as F(x)=x−2510
∴P(27≤x≤33)=F(33)−F(27)
=(33−2510)−(27−2510)
=810−210=610=35
Topper's Solved these Questions
Similar Questions
Following is the distribution function F(x) of a X.

Find P(X≤3),P(2≤X≤5)
View SolutionThe following is the p.d.g. (Probability Density Function) of a continuous random varible X:
f(x)=x32,0<x<8=0, otherwise
(a) Find following the expression for c.d.f. (Cumulative Distribution Function) of X.
(b) Also find its value at x=0.5and9.
View Solution
Knowledge Check
Find the range of the function (i) F(x)=2x2+5, where −3≤x≤2
ARF={y∈R∣−5≤y≤23}.BRF={y∈R∣5≤y≤23}.CRF={y∈R∣5≤y≤13}.DNone of theseWhat is the equivalent definition of the function. given by f(x) ={2xx≤00x<0
Af(x)=|x|Bf(x)=2xCf(x)=|x|+xDf(x)=2|x|Let f(x) and g(x) be two functions given by f(x)=−1|x−1|,−1≤x≤3 and g(x)=2−|x+1|,−2≤x≤2
Then,Afog is differentiable at x=-1 and gof is differentiable at x=1Bfor is differentiable at x=-1 and gof is not differentiable at x=1Cfog is differentiable at x=1 and gof is differentiable at x=-1Dnone of these
For the following distribution function F (X) of a r.v. X
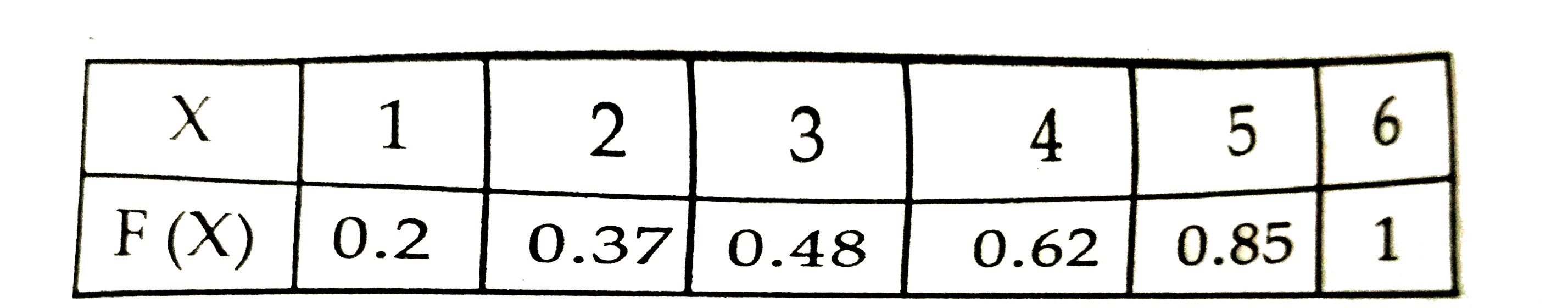
P(3<X≤5)=
View SolutionThe following is the p.d.f (Probability Density Function ) of a continous random variable X :
f(x)=x32,0<x<8
= 0 , otherwise
Find the expression for c.d.f (Cumulative Distribution Function ) of X
View SolutionDiscuss the applicability the Rolle's theorem for the function f(x) = x2 in the interval [2,3].
View SolutionProbability distribution of X is given by
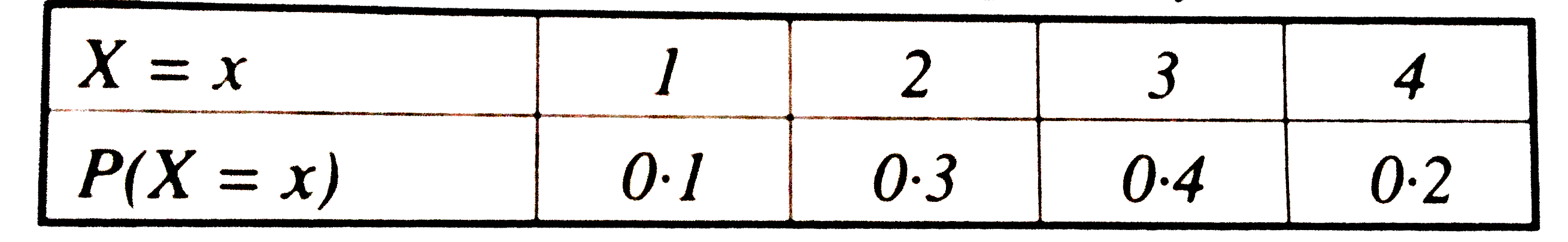
Find P(X≤2) and obtain cumulative distribution function of X.
View SolutionLet f(x) be defined on [-2,2] and is given by
f(x) = {x+1−2≤x≤0x−10≤x≤2, then f (|x|) is defined as
View Solution
