$I f sin {{cot}^{- 1} (x + 1)} = cos ({tan}^{- 1} x),$ then find $x .$

A

$\frac{1}{3}$

B

$\frac{1}{2}$

C

$- \frac{1}{2}$

D

$- \frac{1}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given , $sin [{cot}^{- 1} (x + 1)] = cos ({tan}^{- 1} x)$ . . . (i)
Let ${cot}^{- 1} (x + 1) = θ$
$\Rightarrow sin θ = \frac{1}{\sqrt{x^{2} + 2 x + 2}}$
$\Rightarrow θ = {sin}^{- 1} (\frac{1}{\sqrt{x^{2} + 2 x + 2}})$
${cot}^{- 1} (x + 1) = {sin}^{- 1} (\frac{1}{\sqrt{x^{2} + 2 x + 2}})$

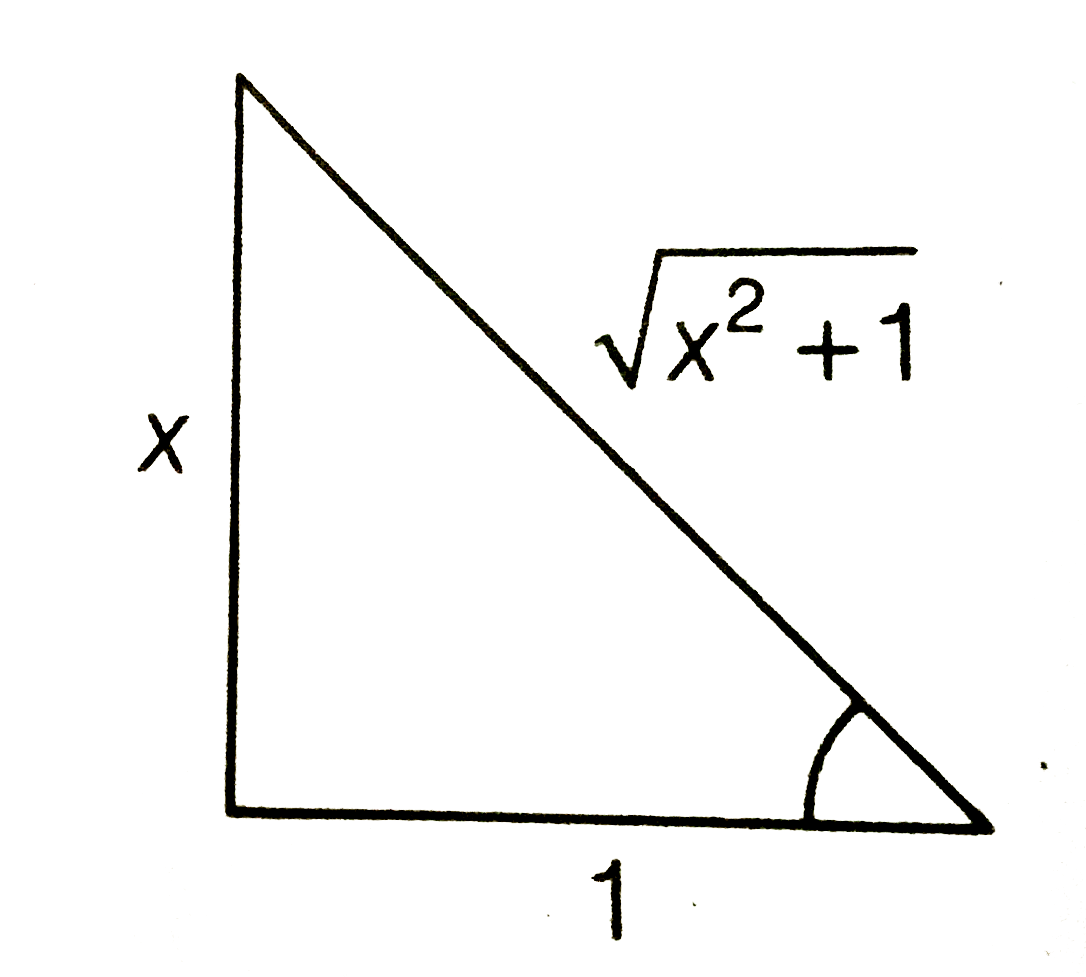
Let ${tan}^{- 1} x = ϕ \Rightarrow tan φ = x$
$\Rightarrow cos φ = \frac{1}{\sqrt{x^{2} + 1}}$
$\Rightarrow φ = {cos}^{- 1} (\frac{1}{\sqrt{x^{2} + 1}})$
$\Rightarrow {tan}^{- 1} x = {cos}^{- 1} (\frac{1}{\sqrt{x^{2} + 1}})$
Now , from Eq . (i) we get
$sin [{sin}^{- 1} (\frac{1}{\sqrt{x^{2} + 2 x + 2}})] = cos [{cos}^{- 1} (\frac{1}{\sqrt{1 + x^{2}}})]$
$\Rightarrow \frac{1}{\sqrt{x^{2} + 2 x + 2}} = \frac{1}{\sqrt{1 + x^{2}}}$
$\Rightarrow \sqrt{x^{2} + 2 x + 2} = \sqrt{1 + x^{2}}$
$\Rightarrow x^{2} + 2 x + 2 = 1 + x^{2}$
$\Rightarrow 2 x + 2 = 1$
$\Rightarrow 2 x = - 1$
$\Rightarrow x = - \frac{1}{2}$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The value of x for which $sin ({cot}^{- 1} (1 + x)) = cos ({tan}^{- 1} x)$ is
A $1 / 2$
B1
C0
D $- 1 / 2$
Question 2 - Select One
If $sin ({cot}^{- 1} (1 - x)) = cos ({tan}^{- 1} (- x))$ , then x is
A1
B $\frac{1}{2}$
C0
D $- \frac{1}{2}$
Question 3 - Select One
$sin {{cot}^{- 1} [cos ({tan}^{- 1} x)]} = ... .$
A $\sqrt{\frac{x^{2} + 2}{x^{2} + 1}}$
B $\sqrt{\frac{x^{2} + 1}{x^{2} + 2}}$
C $\sqrt{x^{2} + 1}$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile