Let PS be the median of the triangle with vertices P(2,2),Q(6,−1)andR(7,3) Then equation of the line passing through (1,−1) and parallel to PS is 2x−9y−7=0 2x−9y−11=0 2x+9y−11=0 2x+9y+7=0
4x -7y -11 =0
2x + 9y +7=0
4x+7y+3=0
2x-9y -11=0
The correct Answer is:B
Coordinates of S (7+61,3−12)=(132,1)
[ since S is the mid-point of line QR]
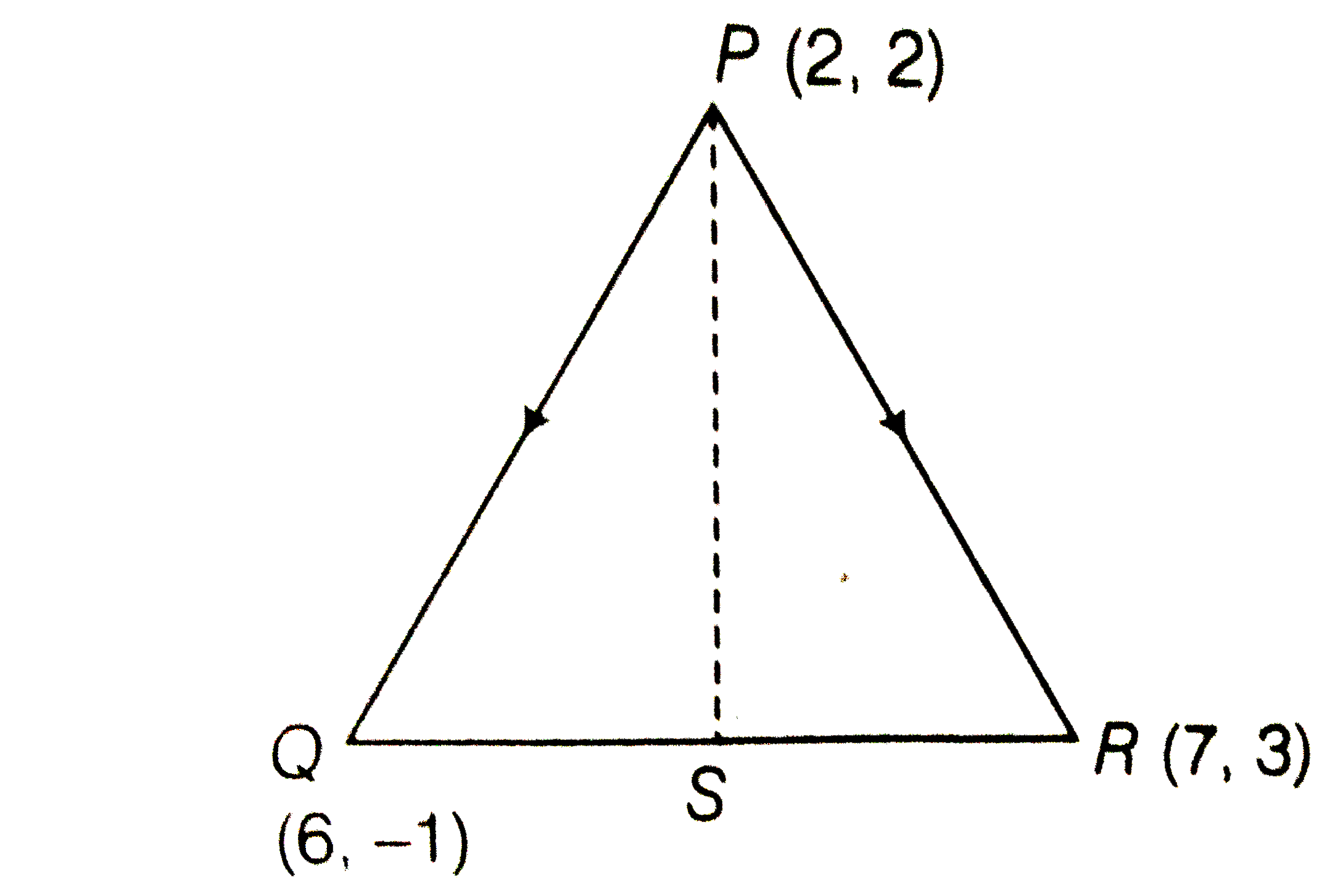
So , the slope of the line PS is −29
Requirred equation passes through (1,-1) and parallel to PS is
y+1=−29(x−1)
⇒2x+9y+7=0
Topper's Solved these Questions
- STRAIGHT LINE BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STRAIGHT LINE EXERCISE - EXERCISE 2(MISCELLANEOUS PROBLEMS)
30 Videos
- SOLVED PAPER 2019BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SOLVED PAPER 2019EXERCISE - MCQS
150 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - MHT CET Corner
3 Videos
Similar Questions
Let PS be the median of the triangle with vertices P(2,2),Q(6,−1)andR(7,3) Then equation of the line passing through (1,−1) and parallel to PS is 2x−9y−7=0 2x−9y−11=0 2x+9y−11=0 2x+9y+7=0
View SolutionLet PS be the median of the triangle with vertices P(2,2),Q(6,−1)andR(7,3) . The equation of the line passing through (1,−1) and parallel to PS is (1) 4x−7y−11=0 (2) 2x+9y+7=0 (3) 4x+7y+3=0 (4) 2x−9y−11=0
View Solution
Knowledge Check
Joint equation of two lines through (2,-1) parallel to two lines 2x2−3xy−9y2=0 is
A2x2−3xy+9y2−5x−24y−7=0B2x2−3xy−9y2−5x−24y−7=0C2x2+3xy−9y2−5x−24y−7=0D2x2+3xy−9y2−5x−24y−7=0The joint equation of pair of lines through (2,−1) and parallel to 2x2+3xy−9y2=0 is
A2x2+3xy+9y2−5x−24y+7=0B2x2+3xy−9y2−5x−24y+7=0C2x2+3xy+9y2−5x−24y−7=0D2x2+3xy−9y2−5x−24y−7=0Let the plane 2x−3y+9z=0 is P, the equation of line passing through (0,1,−1) and lying-in plane 4x−2y+7x+9=0 & parallel to P is:
Ax−3=y−12=z+18Bx−3=y−122=z+18Cx−1−3=y−12=z+18Dx−3=y−111=z+14
Find the equation of the tangent line to the curve y=x2−2x+9 which is parallel to the line 2x−y+7=0
View SolutionFind the equation of the tangent line to the curve y=x2−2x+7 which is parallel to the line 2x−y+9=0
View SolutionFind the equation of a line passing through point (5, 1) and parallel to the line 7x – 2y + 5 = 0.
(a)7x-2y-33=0
(b)6x-8y=0
(c)5x-8y-9=0
(d)None of these
View SolutionFind the equation of the line midway between the parallel lines 9x+6y−7=0 and 3x+2y+6=0
View SolutionThe joint equation of lines passing through the origin and perpendicular to lines represented by 2x2−3xy−9y2=0 is
View Solution
