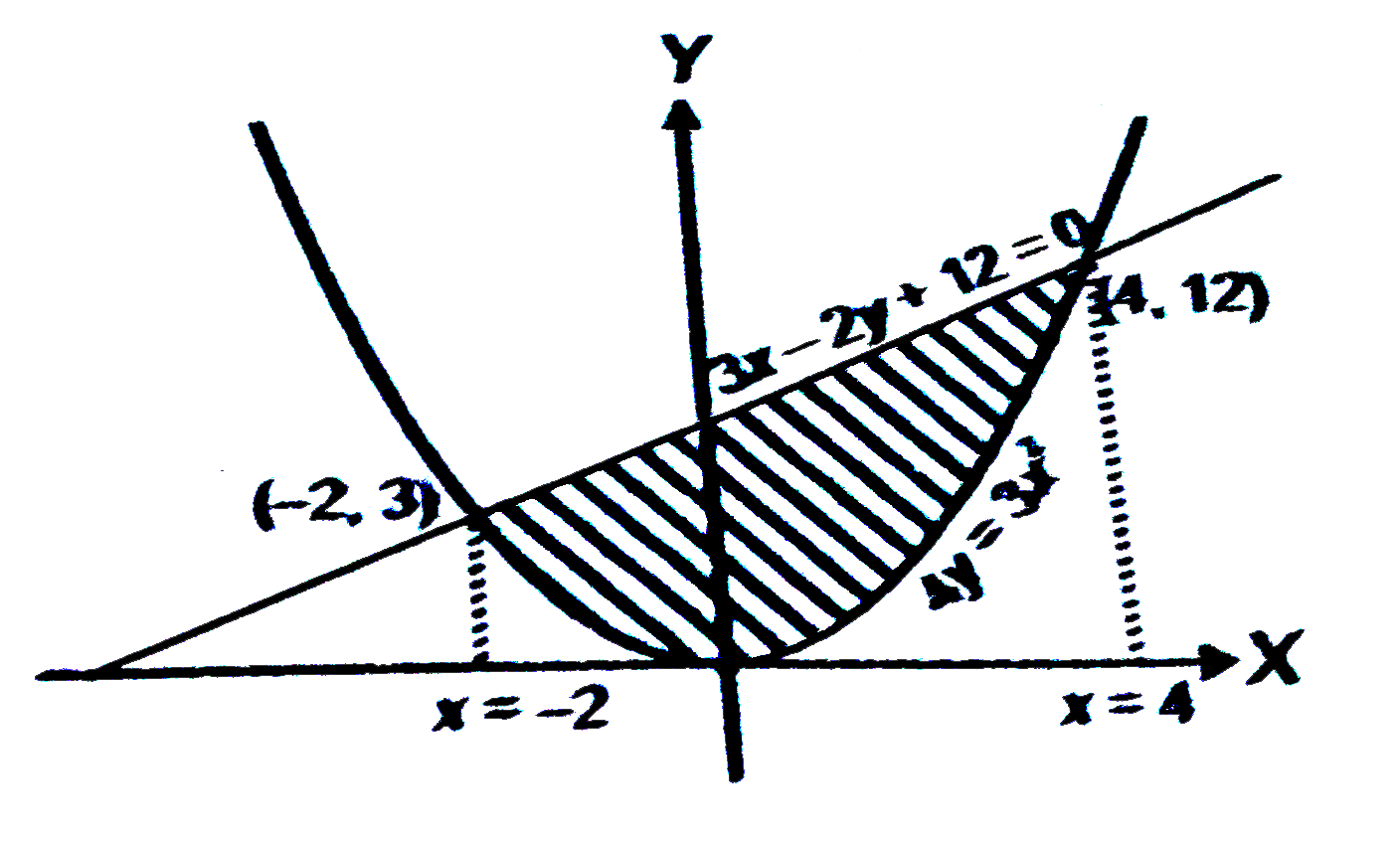
Find the area enclosed between the parabola $4 y = 3 x^{2}$ and the straight line $3 x - 2 y + 12 = 0$

Video Solution

Text Solution

Verified by Experts

Solving $y = \frac{3 x^{2}}{4}$ and $3 x - 2 y + 12 = 0$ , we get $x = - 2, 4$
Area = $\int_{- 2}^{4} [(\frac{3 x + 12}{2}) - \frac{3 x^{2}}{4}]$ dx
$= \frac{3}{4} {[x^{2}]}_{- 2}^{2} + 6 {[x]}_{- 2}^{4} - \frac{3}{4} {[\frac{x^{3}}{3}]}_{- 2}^{4}$
=27 sq. units

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area enclosed by the parabola $y = 3 (1 - x^{2})$ and the x-axis is
A4
B3
C9
D2

AAKASH INSTITUTE-APPLICATION OF INTEGRALS -Assignment Section - I Aakash Challengers Questions

Home
Ask Doubt
Profile