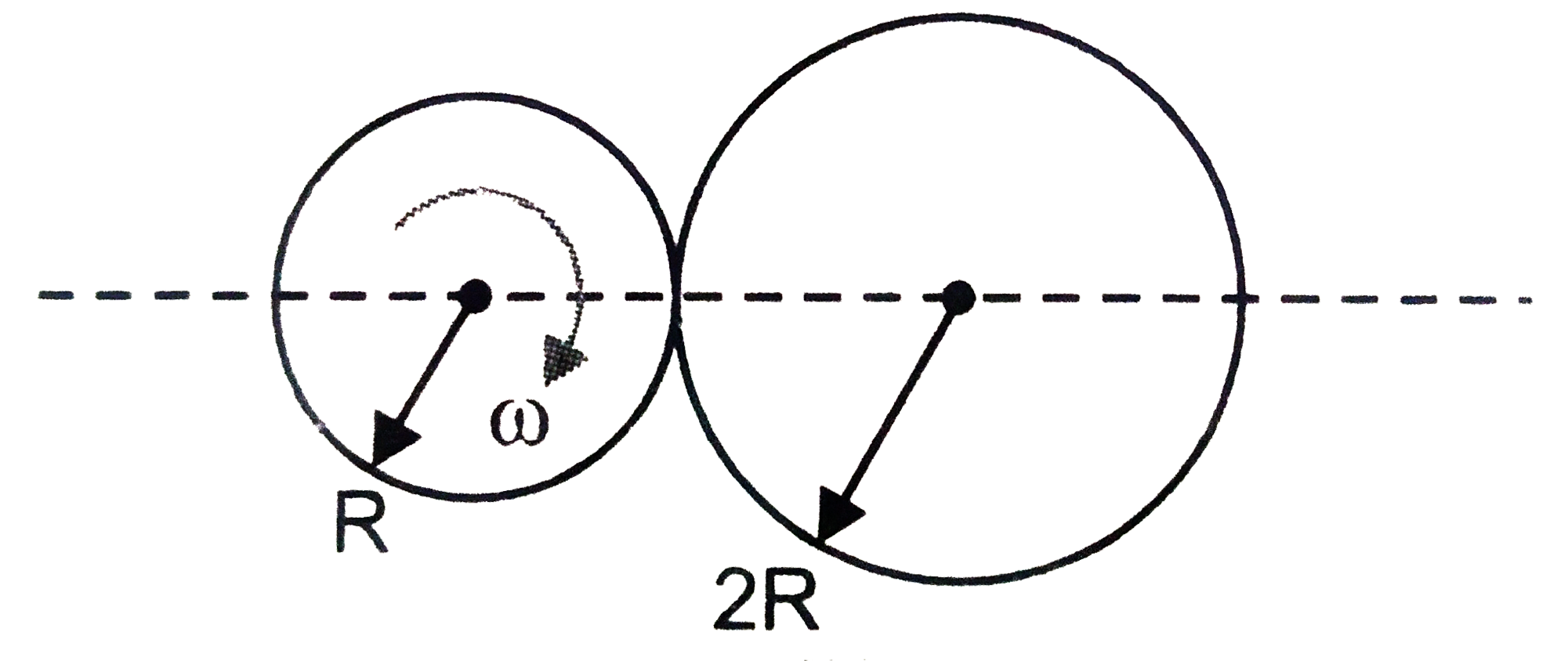
Two discs of radii $R and 2 R$ are pressed against each other. Initially, disc with radius $R$ is rotating with angular velocity $ω$ and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is $I$ and of bigger disc is $2 I$ about their respective axis of rotation. Find the angular velocity of bigger disc after long time.

Video Solution

Text Solution

Verified by Experts

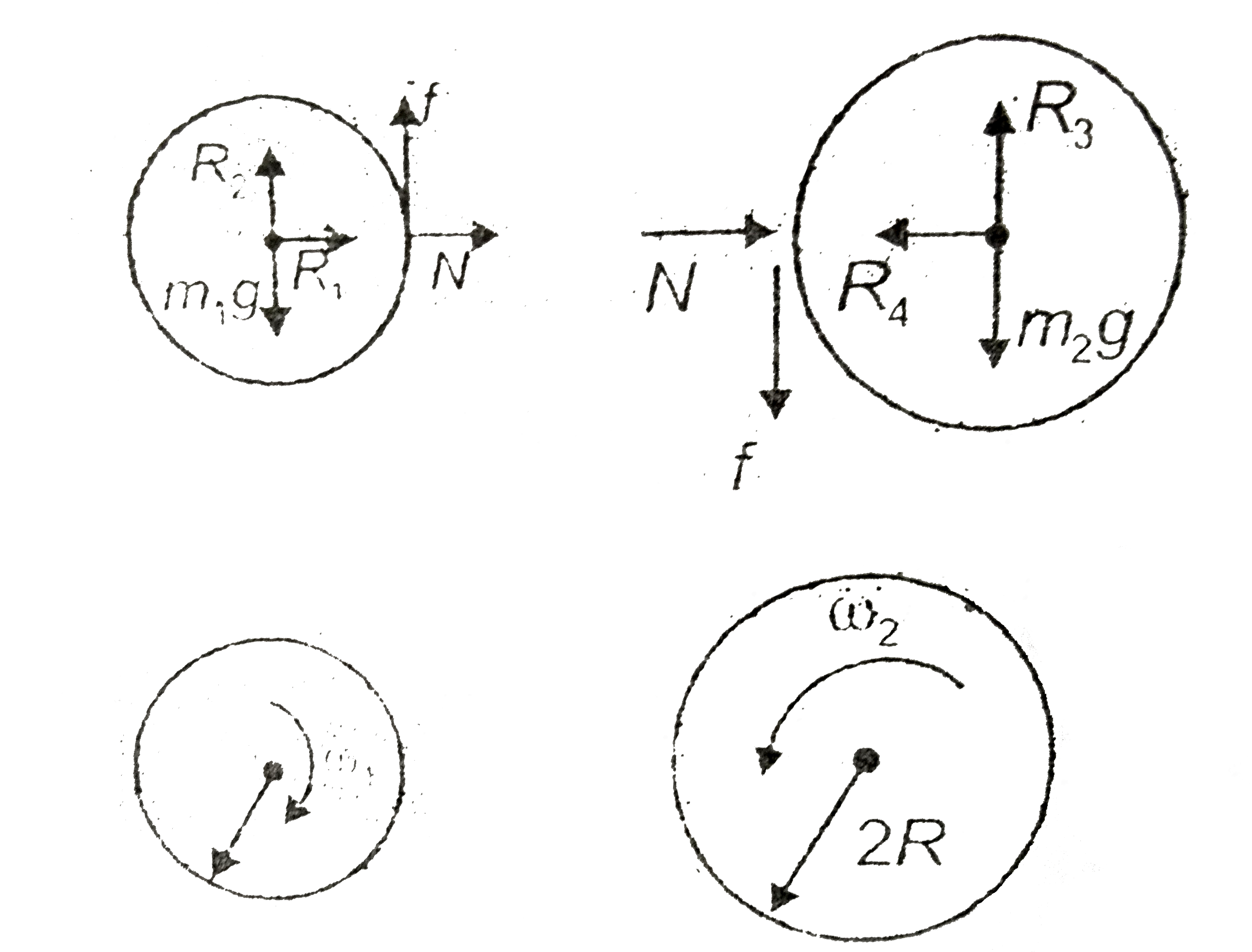
The only force which is producing any torque about the centre of first disk is friciton.
Let the disc rotates with angular velocity $ω_{1}$ and $ω_{2}$ as shown.
Now $ω_{1} R = ω_{2} 2 R$ as the point in contact should have same velocity after slipping stops.
$\Rightarrow ω_{2} = \frac{ω_{1}}{2}$
Now, total angular impulse provided by the friciton is equal to change in angular momentum of the disc
$\int f R d t = l (ω - ω_{1})$
$\int f 2 R d t = 2 l ω_{2}$
$\Rightarrow 2 l (ω - ω_{1}) = 2 l ω_{2}$
$ω_{1} + ω_{2} = ω$
$2 ω_{2} + ω_{2} = ω$
$ω_{2} = \frac{ω}{3}$

Updated on:21/07/2023

A circular disc is rotating about its own axis at uniform rate completes $30$ rotations in one minute.The angular velocity of disc in rad $s^{- 1}$ is
A $2 π$
B $π$
C $\frac{π}{2}$
D $\frac{π}{4} i$
A heavy disc is rotating with uniform angular velocity $ω$ about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
Aincrease
Bdecrease
Cbecomes zero
Dremain unchanged
A circular disc of radius R is rotating about its axis O with a uniform angular velocity $ω {rad s}^{- 1}$ as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is

Azero
B $R ω sin (\frac{θ}{2})$
C $2 R ω sin (\frac{θ}{2})$
D $\sqrt{3} R ω sin (\frac{θ}{2})$