An object starts from rest from the point A to rest at point B on the same straight line at a distance d. It moves over the first part of the distance with an acceleration αm/s2 and for the remainder the retardation βm/s2. Find the time taken to complete the journey.
Method-I
Let C be the position where the speed of object is maximum (v0). For A to C motion is uniformly accelerated and from C to B motion is retarded. We have
d=AC+CB
⇒ d=v202α+v202β (use v2=u2+2as for AC and CB)
⇒ v0=√2αβα+βd
Total time taken
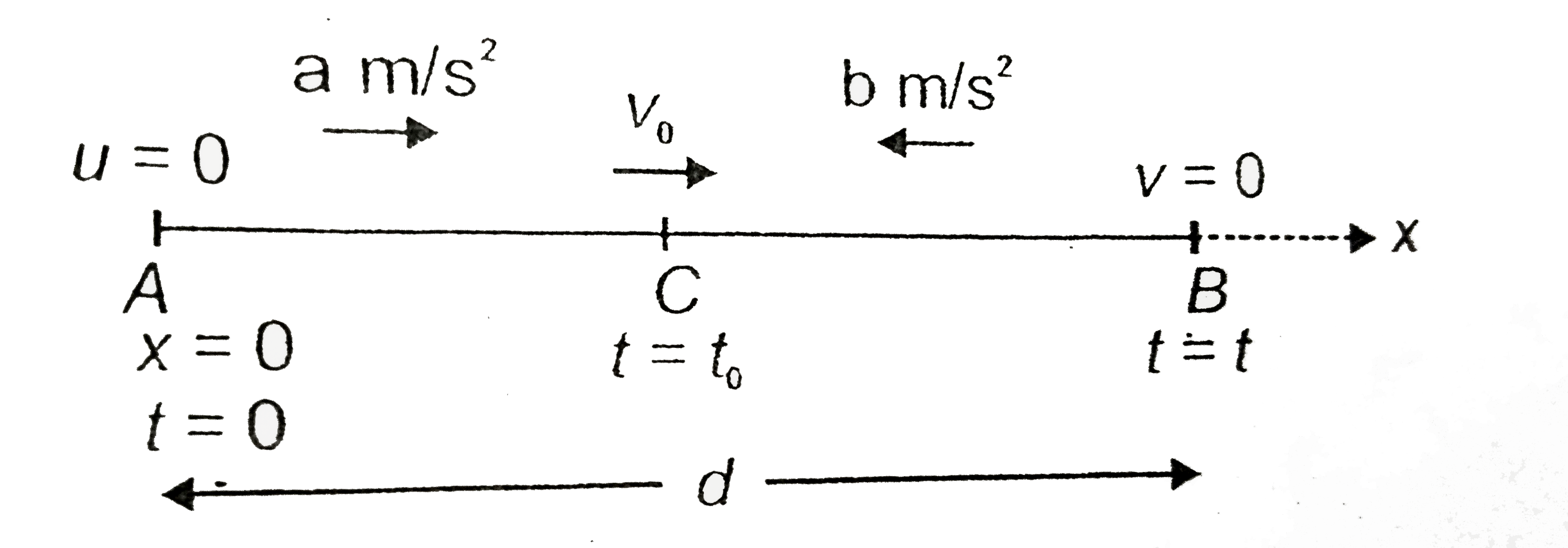
t=tA→C+tC→B
⇒ t=v0α+v0β (use v = u + at for AC and CB)
⇒ t=v0(α+β)αβ=√2αβd(α+β).(α+βαβ)
⇒ t=√2(α+β)αβd
Method II Using the v-t graph
The v-t graph of the motion is shown. For the first part, the slope of v-t graph is equal to α and for the second part slope is equal to −β. We have
Total distance travelled = Area under v-t graph
⇒ d=12v0t ...(i)
Also, t=v0tanθ1+v0tanθ2

⇒ t=v0(1α+1α)
⇒ v0=αβtα+β ...(ii)
From (i) and (ii),
t=√2(α+β)dαβ
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
Knowledge Check
A body travels a distance s in t seconds. It starts from rest and ends at rest . In the first part of the journey , it moves with constant acceleration f and in the second part with constant retardation r. the value of t is given by
A√8s(1f+1r)B2s(1f+1r)C2s1f+1rD√2s(f+r)A body starts from rest with an acceleration 2m/s2 till it attains the maximum velocity then retards to rest with 3m/s2. If total time taken is 10 second, then maximum speed attained is
A12 m/sB8 m/sC6 m/sD4 m/sA particle starts moving along a line from zero initial velocity and comes to rest after moving distance d. During its motion it had a constant acceleration f over 2/3 of the distance, and covered the rest of the distance with constant retardation. The time taken to cover the distance is
A√2d/3fB2√d/3fC√3d/fD√3d/2f
A car starts from rest and accelerates uniformly to a speed 50ms^(-1) over a distance of 250m . Find the acceleration and time taken by the car to cover this distance.
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionA body starts from rest from the origin with an acceleration of 3m/s(2) along the x-axis and 4m/s2 along the y-axis. Its distance from the origin after 2s will be
View SolutionA body starts from rest from the origin with an acceleration of 6m/s2 along the x-axis and 8m/s2 along the y-axis. Its distance from the origin after 4 seconds will be
View SolutionA body moving with uniform acceleration 8m/s2 starts from rest. The distance covered by it in fifth second will be
View Solution
